2010年北京市西城区一模理科数学第8题(选择压轴题):
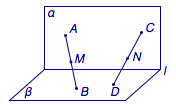
如图,平面$\alpha$与平面$\beta$垂直,直线$l$为两个平面的交线.$A$、$C$是平面$\alpha$内不同的两点,$B$、$D$是平面$\beta$内不同的两点,且$A,B,C,D\not\in l$,$M$、$N$分别是线段$AB$、$CD$的中点,下列判断正确的是( )
A.当$|CD|=2|AB|$时,$M$、$N$两点不可能重合
B.$M$、$N$两点可能重合,但此时直线$AC$与直线$l$不可能相交
C.当$AB$与$CD$相交,直线$AC$平行于$l$时,直线$BD$可以与$l$相交
D.当$AB$、$CD$是异面直线时,$MN$可能与$l$平行
正确答案是 B.
在正式解决这个问题之前,我们先介绍立体几何中非常重要的透视引理(这是我自己的命名):
三个平面两两相交,则三条交线或者互相平行,或者交于一点.
引理的证明是非常简单的,甚至不需要画图就可以直接证明:
设三个平面分别为$\alpha$、$\beta$、$\gamma$,且$\alpha\cap\beta =c$,$\beta\cap \gamma =a$,$\gamma\cap \alpha=b$.
由于直线$a$与直线$b$共面,于是$a$与$b$或者平行,或者相交,讨论如下.
情形一 $a\parallel b$时
此时$$\alpha\cap\beta\cap\gamma =\varnothing,$$于是同在平面$\alpha$内的直线$b$与直线$c$没有公共点,因此$b\parallel c$.根据平行公理,有$$a\parallel b\parallel c,$$即三条交线互相平行.
情形二 $a\cap b=P$时
此时$$\alpha\cap\beta\cap\gamma=P,$$于是$$\left(\gamma\cap\alpha\right)\cap \left( \alpha\cap\beta\right) =P,$$即$b\cap c=P$,从而$$a\cap b\cap c=P,$$即三条交线交于一点.
综上,引理得证.
回到原问题,依次考虑四个选项.
选项 A,如图1,取与$l$平行的平面,与$\alpha$和$\beta$分别相交,在两条交线上取一条线段$AB$,然后将这条线段绕其中点$M$旋转,那么在旋转过程中必然可以找到长度是起始长度$2$倍的位置,即线段$CD$.因此选项 A 错误.
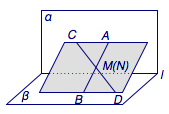
选项 B,由对选项 A 的分析可知,$M$、$N$可以重合,如图2,若$M$与$N$重合,那么$AB$与$CD$互相平分,因此$ADBC$为平行四边形.对平行四边形所在平面与$\alpha$、$\beta$应用引理即得$$AC\parallel BD\parallel l,$$因此选项 B 正确.
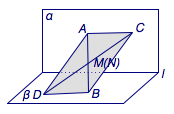
图2 选项B的证明
选项 C,若$AB$与$CD$相交,那么它们构成一个平面,对该平面与$\alpha$、$\beta$应用引理即得$$AC\parallel l\parallel BD,$$因此选项 C 错误.
选项 D,如图3,当$MN$与$l$平行时,将线段$AB$沿向量$\overrightarrow {MN}$平移到$A'B'$,则根据对选项 B 的分析,有$$CA'\parallel B'D\parallel l,$$又$$AA'\parallel BB'\parallel MN\parallel l,$$于是在平面$\alpha$内,过$A'$的平行线$CA'$与$AA'$重合,于是$A$在平面$A'CB'D$内,类似的,$B$也在平面$A'CB'D$内,因此$AB$与$CD$共面.
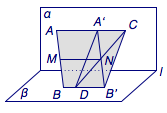
图3 选项D的证伪
注一 条件“平面$\alpha$与平面$\beta$垂直”是多余的.
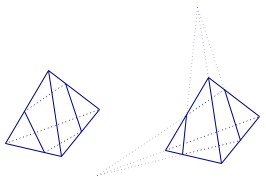
注二 事实上,立体几何作图时是否遵从透视引理直接影响立体感,如图4.