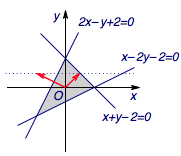
2014年高考安徽卷理科数学第5题:
已知$x,y$满足约束条件$\begin{cases} x+y-2\leqslant 0,\\x-2y-2 \leqslant 0,\\2x-y+2 \geqslant 0,\end{cases} $若$z=y-ax$取得最大值的最优解不唯一,则实数$a$的值为( )
A.$-\dfrac 12$或$-1$
B.$2$或$\dfrac 12$
C.$2$或$1$
D.$2$或$-1$
正确答案是 D.
解 我们一般将目标函数$z=y-ax$化为直线$y=ax+z$,从而将$z$看作直线的截距来解决问题.实际上,在学习了向量数量积的坐标运算后,我们还可以利用向量给出更简明的解决方案.
将目标函数$z=y-ax$,看作向量$(x,y)$与向量$(-a,1)$的数量积.由于向量$(-a,1)$的模为定值,于是数量积的大小取决于可行域内的点在向量$(-a,1)$上的有向投影的大小.
在本题中,目标函数取得最大值的最优解不唯一,这就意味着向量$(-a,1)$与可行域的某个边界垂直,且该边界上的点的有向投影是最大的.不难确定,符合条件的边界为直线$x+y-2=0$和$2x-y+2=0$,于是它们的纵坐标为$1$的法向量分别为$(1,1)$以及$(-2,1)$.
下面给出两道练习题.
练习1、由点$A(6,2)$,$B(1,1)$,$C(1,5)$围成的三角形为可行域,若目标函数$z=ax+y$取最大值的最优解有无穷多个,则$a$的值为_______.($\dfrac 35$)
练习2、(2015年东北三校联考)变量$x,y$满足约束条件$\begin{cases} y\geqslant -1,\\x-y\geqslant 2,\\3x+y\leqslant 14,\end{cases} $若使$z=ax+y$取得最大值的最优解有无穷多个,则实数$a$的取值集合是_______.($\{-1,3\}$)
注 解题中用到了直线$Ax+By+C=0$的一个法向量为$(A,B)$,这个结论是显然而常用的.