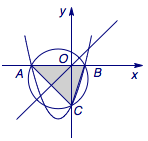
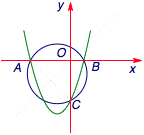
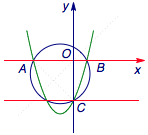
函数$y=x^2+ax+b$的图象与坐标轴交于三个不同的点$A$、$B$、$C$，已知$\triangle ABC$的外心在直线$y=x$上，求$a+b$的值．
正确答案是$-1$．
解 作出三角形$ABC$的外接圆$M$，我们发现$M$实际上是过抛物线与$x$、$y$轴交点的曲线，因此可以尝试用交点曲线系解决问题．
尝试用交点曲线系写方程
事实上，抛物线方程为$$F:x^2+ax+b-y=0,$$而$x$、$y$轴的方程为$$G:xy=0,$$此时我们发现利用常规的交点曲线系$f(x,y)+\lambda g(x,y)=0$得到的方程$$(x^2+ax+b-y)+\lambda\cdot xy=0$$不可能形成圆．
那么问题出在哪里？又该怎样解决呢？
由于圆的方程的特点，我们知道问题出在交叉项$xy$上．因此需要仔细思考交点$C(0,b)$除了用$x=0$描述，是否还有其他方法？
转化思路后调整方程
到这里，答案几乎是显然的，应该采用$y=b$描述，此时可以将交点曲线系写为$$(x^2+ax+b-y)+\lambda \cdot y(y-b)=0,$$当方程表示圆时，$\lambda=1$，于是再由圆心在直线$y=x$上，可得关于$x$、$y$的一次项的系数相同，即$$a=-1-b,$$从而$a+b$的值为$-1$．
另法一 利用圆幂定理
显然圆心的坐标为$M \left( -\dfrac a2,-\dfrac a2\right) $，于是对原点$O$应用圆幂定理有$$\overrightarrow {OA}\cdot \overrightarrow {OB}=OM^2-MC^2,$$即$$b=\left(-\dfrac a2\right)^2+\left(-\dfrac a2\right)^2-\left[\left(-\dfrac a2\right) ^2+ \left( -\dfrac a2-b\right)^2\right],$$整理即得$$a+b=-1.$$
另法二 利用圆的一般方程
设$A(x_1,0)$，$B(x_2,0)$，圆的方程为$x^2+y^2+mx+my+n=0$，而$C(0,b)$，于是$$\begin{cases} x_1^2+mx_1+n=0,\\x_2^2+mx_2+n=0,\\b^2+mb+n=0, \end{cases} $$由于$x_1,x_2$同时是方程$$x^2+ax+b=0$$和方程$$x^2+mx+n=0$$的两个根，于是$m=a$且$n=b$，因此$$b^2+ab+b=0,$$即$$a+b=-1.$$
注一 本题源自2008年高考江苏卷第18题：
在平面直角坐标系$xOy$中，记二次函数$f(x)=x^2+2x+b$（$x\in\mathcal R$）与坐标轴有三个交点．经过三个交点的圆记为$C$．
（1）求实数$b$的取值范围；
（2）求圆$C$的方程；
（3）问圆$C$是否经过定点（其坐标与$b$无关）？证明你的结论．
注二 有关交点曲线系的更多题目可以参考《每日一题[57] 交点曲线系》，以及《每日一题[33] 交点曲线系》．