2012年高考上海卷理科数学第14题(填空压轴题):
如图,\(AD\)与\(BC\)是四面体\(ABCD\)中互相垂直的棱,\(BC=2\).若\(AD=2c\),且\(AB+BD=AC+CD=2a\),其中\(a\)、\(c\)为常数,则四面体\(ABCD\)的体积的最大值是_______.
正确答案是\(\dfrac{2c}3\sqrt{a^2-c^2-1}\).
解 首先对于用对边来描述的四面体,我们一般都将其放入平行六面体中,利用平行六面体,如《每日一题[193] 四面体的外接平行六面体》,如图.

这样我们就有对边描述的四面体体积公式\[V_{ABCD}=\dfrac 16\cdot AD\cdot BC\cdot d(AD,BC)\cdot \sin\langle AD,BC\rangle,\]其中\(d(AD,BC)\)表示异面直线\(AD\)与\(BC\)的距离,\(\langle AD,BC\rangle\)表示异面直线\(AD\)与\(BC\)所成的角.
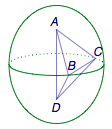
回到本问题,\(AB+BD=AC+CD=2a\)描述的事实为\(B\)点和\(C\)点到两定点\(A\)、\(D\)的距离之和为\(2a\),于是点\(B\)、\(C\)都在以\(A\)、\(D\)为焦点的椭球上,如图.利用椭球,不难对四面体\(ABCD\)的顶点\(B\)和\(C\)进行“GPS定位”.
由于\(AD\perp BC\),于是\(BC\)必然为某个垂直于\(AD\)的平面截椭球形成的圆的弦,且\(d(AD,BC)\)即该圆的圆心到弦的距离.
我们知道,当弦长固定时,圆的半径越大,圆心到弦的距离越大.于是当\(BC\)为过线段\(AD\)中点的截面的弦时,四面体\(ABCD\)的体积最大,此时由垂径定理不难得到\[d(AD,BC)=\sqrt{a^2-c^2-1},\]进而可以计算得\[V_{ABCD}=\dfrac{2c}3\sqrt{a^2-c^2-1}.\]
下面给出一道练习.
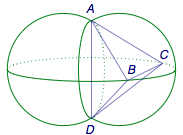
已知\(AD\)与\(BC\)是四面体\(ABCD\)中互相垂直的棱,若\(BC=2\),\(AD=4\),且\(\angle ABD=\angle ACD=60^\circ\),则四面体\(ABCD\)的体积的最大值是_______.
答案是\(\dfrac{4\sqrt{11}}3\).
提示 如图,四面体\(ABCD\)的外接球是固定的.



Pingback引用通告: 每日一题[880]对边描述的四面体 | 数海拾贝内容系统
Pingback引用通告: 每日一题[880]对边描述的四面体 | Math173
Pingback引用通告: 每日一题[304] 小橄榄长成大南瓜 | Math173