每日一题[21] 代数条件的直观化

今天继续带来一道代数条件直观化的试题．原题是2015年北京市海淀区高三期末文科压轴题．

已知数列$\{a_n\}$是公差为$d$，首项$a_1=1$的等差数列，问是否存在实数$d$使得数列$\left\{\dfrac{1}{a_n}\right\}$满足：可以从中取出无限多项，并按原来的先后次序排成一个等差数列？若存在，求出所有满足条件的$d$的值；若不存在，说明理由．

满足条件的$d$只有一个，为$0$．

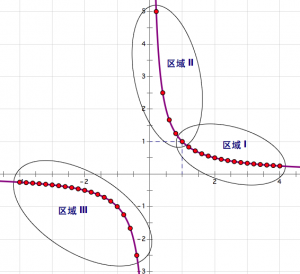
如图，按$d$的正负讨论．

当$d>0$时，$\left\{\dfrac{1}{a_n}\right\}$的子列在区域I中，于是数列$\left\{\dfrac{1}{a_n}\right\}$有下界$0$．考虑到$\left\{\dfrac{1}{a_n}\right\}$的子列按原有的先后次序排列，若能组成等差数列，从区域I中自左向右取项时公差为负数，一定没有下界，矛盾；

当$d<0$时，$\left\{\dfrac{1}{a_n}\right\}$的子列在区域II及区域III中．考虑到$\left\{\dfrac{1}{a_n}\right\}$的子列按原有的先后次序排列，因此不可能同时包含区域II及区域III中的项．区域II中的项数有限，而按自右往左在区域III中取项时，公差为正数，与有上界矛盾．

当$d=0$时，显然符合题意．

综上，满足条件的$d$只有一个，为$0$．