每日一题[14] 共圆的向量表达

共线向量和共圆向量是向量问题中两种最重要的向量．共线向量的表达一般利用 $$\overrightarrow{OP}=\lambda\overrightarrow{OA}+(1-\lambda)\overrightarrow{OB}$$ 进行，那么如何恰当的表达共圆向量呢？ 如图，已知扇形$AOB$的圆心角为$120^\circ$，$P$为弧$AB$上一点，$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$．求$x+y$的取值范围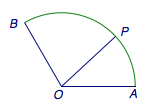． 法一（代数方法） 不妨设扇形的半径为$1$．根据已知条件，有 $$\overrightarrow{OP}\cdot\overrightarrow{OP}=\left(x\overrightarrow{OA}+y\overrightarrow{OB}\right)\cdot\left(x\overrightarrow{OA}+y\overrightarrow{OB}\right),x,y\geqslant 0$$ 于是 $$1=x^2-xy+y^2.$$ 因此 $$xy=\frac{(x+y)^2-1}3\leqslant \left(\frac{x+y}2\right)^2,$$ 解得 $$x+y\leqslant 2,"=" iff x=y=1.$$ 又 $$(x+y)^2\geqslant x^2-xy+y^2=1,$$ 于是 $$x+y\geqslant 1,"="\  iff\ xy=0.$$ 这样，就得到$x+y$的取值范围是$[1,2]$．

注　iff表示当且仅当．

 法二（几何方法） 连接$AB$，作弧$AB$的切线$l$使得$l\parallel AB$，设切点为$M$．连接$OM$交$AB$于$N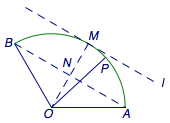$． 我们熟知，若点$P$落在直线$AB$上，则 $$x+y=1.$$ 而由已知条件不难推知$OM=2ON$，于是若点$P$落在切线$l$上，则 $$x+y=2.$$ 事实上，弧$AB$落在直线$AB$和切线$l$之间，于是$x+y$的取值范围是$[1,2]$．

想想看，如果求$x+2y$的取值范围，该如何思考呢？