【初级】
如图，在\({\rm Rt}\triangle ABC\)中，\(\angle C=90^\circ\)，\(AC:CB=1:3\)，且\(E,D\)是\(BC\)三等分点，求证：\(\angle 1+\angle 2=45^\circ\)．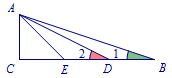
分析 \(\angle 1\)与\(\angle 2\)目前处于分离的状态，一般处理这种题目方向有两种，①把两个角放到一个三角形中：通过比值可得到\(\triangle AED\backsim \triangle BEA\)，则\(\angle 2=\angle EAB\)，这个方法相似不太好找，不推荐；②把它们组成一个大角：根据已知条件中的比值，可以构建方格，两个角通过全等很容易组合成大角，这样问题就会非常简单了．
解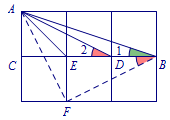
根据\(\triangle ADC\cong \triangle FBE\)，可得\(\angle 2=\angle EBF\)．
因为\(\triangle AFB\)为等腰直角三角形，从而得到\(\angle 1+\angle 2=45^\circ\)．
【升级】
（2009年海淀八年级上期末27题最后一问）
在平面直角坐标系\(xOy\)中，\(A(2,1),B(3,1),C(6,0)\)，点\(P\)在\(x\)轴上，\(\angle APB=20^\circ\)，求\(\angle A+\angle B\)的度数．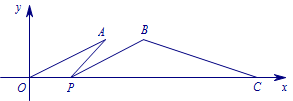
解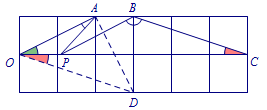
因为\(\angle C=\angle DOP\)，\(\triangle AOD\)为等腰直角三角形，
所以\(\angle AOP+\angle DOP=45^\circ\)．
因为\(\angle APO+\angle BPC=160^\circ\)，
再根据三角形内角和，可得\(\angle A+\angle B=155^\circ\)．
点评 若\(\tan\angle A=\dfrac 12\)，\(\tan \angle B=\dfrac 13\)，（\(\angle A,\angle B\)均为锐角）则\(\angle A+\angle B=45^\circ\)．这个结论在小题中可以直接使用，解答题中需要证明．