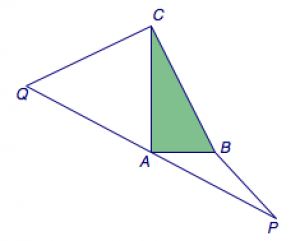
如图,在直角三角形\(ABC\)中,已知\(BC=a\).若长为\(2a\)的线段\(PQ\)以点\(A\)为中点,问\(\overrightarrow{PQ}\)与\(\overrightarrow{BC}\)的夹角\(\theta\)取何值时,\(\overrightarrow{BP}\cdot\overrightarrow{CQ}\)的值最大?并求出这个最大值.
\[\begin{split}\overrightarrow{BP}\cdot\overrightarrow{CQ}&=\left(\overrightarrow{AP}-\overrightarrow{AB}\right)\cdot\left(\overrightarrow{AQ}-\overrightarrow{AC}\right)\\&=\overrightarrow{AP}\cdot\overrightarrow{AQ}-\overrightarrow{AB}\cdot\overrightarrow{AQ}-\overrightarrow{AP}\cdot\overrightarrow{AC}+\overrightarrow{AB}\cdot\overrightarrow{AC}\\&=-a^2+\overrightarrow{AP}\cdot\left(\overrightarrow{AB}-\overrightarrow{AC}\right)\\&=-a^2+\overrightarrow{AP}\cdot\overrightarrow{CB}\\&\leqslant -a^2+a^2=0,\end{split}\]
等号当且仅当\(\overrightarrow{AP}\)与\(\overrightarrow{CB}\)同向,即\(\theta=0\)时取得.