每日一题[223] 论证与构造

2014年高考辽宁卷理科数学第12题（选择压轴题，有不改变本质的改动）：

已知定义在\([0,1]\)上的函数\(f(x)\)满足：

①  \(f(0)=f(1)=0\)；

②  \(\forall x,y\in [0,1] \land x\neq y,\left|f(x)-f(y)\right|<\dfrac 12|x-y|\)；

若对所有\(f(x)\)均有\(\forall x,y\in [0,1],\left|f(x)-f(y)\right|<k\)成立，则\(k\)的最小值为（        ）

A．\(\dfrac 12\)

B．\(\dfrac 14\)

C．\(\dfrac{1}{2\pi}\)

D．\(\dfrac 18\)

正确答案为 B．

解    条件①的含义为函数图象的端点是确定的；

条件②的含义为函数图象上任意两点的斜率\(\dfrac{f(x)-f(y)}{x-y}\)在\(\left(-\dfrac 12,\dfrac 12\right)\)之间，也就是说函数图象的增长/减少速度是受限的；

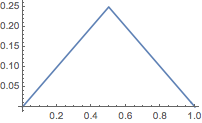
题目要求的\(k\)的最小值也即为函数\(f(x)\)的值域长度的最大值，由于函数图象从\((0,0)\)出发，最终要回到\((1,0)\)，于是考虑\(f\left(\dfrac 12\right)\)．显然在区间\(\left[0,\dfrac 12\right]\)上，函数值改变量的上界为\(\dfrac 14\)．于是函数\(f(x)\)的值域长度的最大值为\(\dfrac 14\)，如图．

下面进行代数描述：

一方面，当\(f(x)\)的图象无限接近函数\[y=\dfrac 14-\dfrac 12\left|\dfrac 12-x\right|, x\in [0,1]\]的图象时，函数\(f(x)\)的值域长度无限接近于\(\dfrac 14\)；

另一方面，若\(f(x)\)的值域长度大于或等于\(\dfrac 14\)，则必然存在\(m\in (0,1)\)使得\[\left|f(m)\right|\geqslant \dfrac 14,\]

此时若\(m\in\left(0,\dfrac 12\right]\)，则令\(x=m\land y=0\)即可推出\[\left|f(m)-f(0)\right|<\dfrac 12\left|m-0\right|,\]矛盾．

类似的，当\(m\in\left(\dfrac 12,1\right)\)，可以令\(x=m\land y=1\)推出矛盾．

因此所求的\(k\)的最小值为\(\dfrac 14\)．