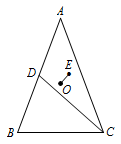
如图，\(\triangle ABC\)的外心为\(O\)，\(AB=AC\)，\(D\)是\(AB\)的中点，\(E\)是\(\triangle ACD\)的重心．证明：\(OE\perp CD\)．
我们先来看一题：
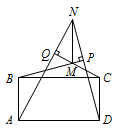
如图，已知矩形\(ABCD\)，\(N\)为平面上一点，连接\(AN,DN\)均与\(BC\)相交，作\(BP\perp DN\)，\(CQ\perp AN\)，两条垂线交点为\(M\)．求证：\(MN\perp BC\)．
题干中两条垂线段交于点\(M\)，求证经过点\(M\)的线段与另一条线段垂直，由此想到三角形垂心的唯一性．
过点\(N\)作\(NE\parallel AB\)，使得\(NE=AB\)，则\(NE\parallel DC\)，\(NE=DC\)．
连接\(BE,CE\)，则四边形\(ABEN\)和四边形\(CDNE\)均为平行四边形．
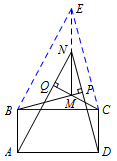
所以\(BP\perp CE\)，\(CQ\perp BE\)，
则\(\triangle EBC\)中，\(M\)为其垂心，所以\(EM\perp BC\)．
由\(EN\parallel AB\)，可得\(EN\perp BC\)，
所以点\(E,N ,M\)三点共线，
所以\(NM\perp BC\)．
再来看本题，连接\(AO\)并延长，交\(CD\)于点\(H\)，连接\(OD\)．
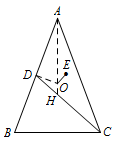易得\(AH\perp BC\)，\(OD\perp AB\)，所以能否构造三角形使得点\(O\)为其垂心很关键．
显然点\(H\)为\(\triangle ABC\)的重心，则\(\dfrac {DH}{HC}=\dfrac 12\)；取\(CD\)中点\(G\)，则\(\dfrac {DH}{HG}=2\)．
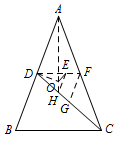连接\(DE\)并延长，交\(AC\)于点\(F\)，则\(DE\parallel BC\)；
连接\(EH,FG\)，则\(\dfrac {DH}{HG}=\dfrac {DE}{EF}=2\)，
\(\therefore EH\parallel FG \parallel AB\)．
\(\therefore O\)为\(\triangle DEH\)的垂心，
\(\therefore OE \perp CD\)．
注 三角形三条高所在的直线交于一点，此点称为三角形的垂心，所以可根据“垂心的唯一性”来证明线段互相垂直．