1、函数\(f(x)=\left|7x-\sqrt{4x^2-9}\right|\)的最小值为_______.
2、若\(\tan x=2\tan\dfrac{\pi}{5}\),则\(\dfrac{\cos\left(x-\dfrac{3\pi}{10}\right)}{\sin\left(x-\dfrac{\pi}{5}\right)}=\)_______.
3、已知等腰直角三角形\(ABC\)中,\(AC=BC=4\),\(D\)为\(AC\)的中点,点\(P\)、\(Q\)是斜边\(AB\)上的动点,且\(PQ=2\sqrt 2\).当\(P\)、\(Q\)在边\(AB\)上运动时,四边形\(PQCD\)周长的最小值是_______.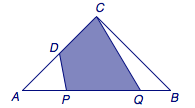
4、抛物线\(y^2=2x\)的内接三角形\(ABC\)的三条边所在直线与抛物线\(x^2=2y\)均相切,设\(A\)、\(B\)两点的纵坐标分别为\(a\)、\(b\),则\(C\)点的纵坐标为________.(用\(a\)、\(b\)表示)
5、已知圆\(O:x^2+y^2=r^2(r>0)\)和圆\(C:(x-4)^2+(y+3)^2=18\),对于圆\(O\)上任意一点\(P\),圆\(C\)上均存在两点\(A\)、\(B\),使得\(\angle APB\)为钝角,则\(r\)的取值范围是_______.
6、四边形\(ABCD\)中,\(\angle ABC=\angle ACB=45^\circ\),\(\angle ADC=75^\circ\),\(AD=5\sqrt 2\),\(CD=6\),则\(BD\)的长为_______.
7、已知\(a,b,c>0\),求证:\((a+b)^2+(a+b+4c)^2\geqslant \dfrac{100abc}{a+b+c}\).
参考答案
1、\(\dfrac{9\sqrt 5}2\) 提示 令\(x=\dfrac{3}{2\cos\theta}\).
2、\(3\)
3、\(2+2\sqrt 2+2\sqrt 5\) 提示 如图.
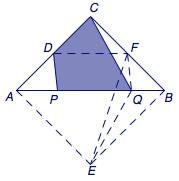
4、\(-a-b\)
5、\((0,1)\) 提示 对圆\(C\)张角为钝角的圆的轨迹是一个圆环(不包含边界).
6、\(2\sqrt{19}\) 提示 如图.
7、证明 由于\[\begin{split}(a+b)^2+(a+b+4c)^2&\geqslant \left(2\sqrt{ab}\right)^2+\left(2\sqrt{(a+b)\cdot 4c}\right)^2\\&=4ab+16bc+16ca,\end{split}\]而根据柯西不等式,有\[\left(4ab+16bc+16ca\right)\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)\geqslant (2+4+4)^2=100,\]因此原不等式得证.

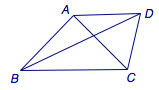
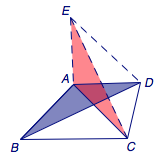
第六题答案有疑问
答案没问题.