每日一题[3700]举棋不定

2025年2月湖北省武汉市高三调研数学考试 #10

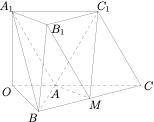
如图，以 $A_1,B_1,C_1,A,B,C$ 为顶点的六面体中，四边形 $AA_1 C_1 C$ 为菱形，$B_1 C_1 \parallel BC$，$B_1 C_1=\dfrac 1 2 BC$，$\angle C_1 CA=60^{\circ}$，$AC=2$，$AB=2$，$\angle BAC=120^{\circ}$，则[[nn]]

A．$AC\perp A_1 B$

B．$AC_1 \parallel ~\text{平面}~A_1 BB_1$

C．当 $A_1 B=\sqrt 6$ 时，二面角 $A_1-AB-C$ 的正弦值为 $\dfrac{\sqrt 5}5$

D．当 $A_1 B=\sqrt 3$ 时，此六面体的体积为 $\dfrac{5\sqrt 3}4$

答案    ABD.

解析    对于选项 $\boxed{A}$，延长 $CA$ 到 $O$，且 $AO=1$，则 $A_1O\perp OC$ 且 $BO\perp OC$，因此 $OC\perp OA_1B$，从而 $AC\perp A_1B$，选项正确；

对于选项 $\boxed{B}$，设 $M$ 为 $BC$ 中点，连接 $MA,MC_1$，则 $B_1C_1$ 与 $BM,MC$ 均平行且相等，于是 $BB_1\parallel MC_1$，$A_1B_1\parallel AM$，从而 $A_1BB_1\parallel AMC_1$，进而 $AC_1\parallel A_1BB_1$，选项正确；

对于选项 $\boxed{C}$，由于 $OA_1=OB=\sqrt 3$，当 $A_1B=\sqrt 6$ 时，有 $\angle A_1OB=90^\circ$，设二面角 $A_1-AB-C$ 的大小为 $\theta$，根据面积射影定理，有

$$|\cos\theta|=\dfrac{[\triangle OAB]}{[\triangle A_1AB]}=\dfrac{\sqrt 3}{\sqrt{15}}\implies \sin\theta=\dfrac{2}{\sqrt{5}},$$ 选项错误；

对于选项 $\boxed{D}$，当 $A_1B=\sqrt 3$ 时，有 $\angle A_1OB=60^\circ$，此六面体的体积

$$\begin{split} V&=[B-AMB_1A_1]+[A_1B_1C_1-AMC]\\ &=5[C_1-AMC]\\ &=5\cdot \dfrac 13\cdot [\triangle AMC]\cdot d(A_1,OB)\\ &=5\cdot \dfrac13\cdot \dfrac{\sqrt 3}2\cdot \dfrac 32\\ &=\dfrac{5\sqrt 3}4,\end{split}$$ 选项正确；

综上所述，正确的选项是 $\boxed{A}$ $\boxed{B}$ $\boxed{D}$．