说明 文科考生做前5题，理科考生做后5题，每题20分， 共100分．
1、设关于\(x\)的方程\(x^2-ax+2a-2=0\)在区间\(\left[0,\dfrac 32\right]\)内有根，求实数\(a\)的取值范围．
2、设\(a,b,c\)满足\(a+b+c=a^3+b^3+c^3=0\)，\(n\)为任意自然数，求\(a^{2n+1}+b^{2n+1}+c^{2n+1}\)的值．
3、证明：若\(n\)为不小于\(2\)的自然数，\(t\)为实数且\(\sin\dfrac{t}{2}\neq 0\)，则\[\sum_{k=1}^n\left(1+\sum_{p=1}^{k-1}2\cos pt\right)=\left(\dfrac{\sin\frac{nt}2}{\sin\frac t2}\right)^2.\]
4、一个等腰梯形的腰和底的长分别为\(\sqrt 2\)和\(3\)，求这个梯形面积的最大值．
5、求出所有实数\(x\)，使得\(\dfrac{x^2+4x-1}{7x^2-6x-5}\)与\(\dfrac{1-x}{1+x}\)同时为整数．
6、顶点为\(A\)的等腰三角形\(ABC\)的角\(B\)的平分线交\(AC\)于\(D\)，已知\(BC=BD+AD\)，求角\(A\)的度数．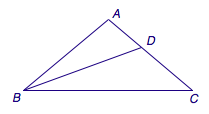 
7、设\(a,b,c\)是实数，方程\(x^3+ax^2+bx+c=0\)有\(3\)个正根，证明\(2a^3+9c\leqslant 7ab\)，并且等号成立当且仅当这\(3\)个正根相等．
参考答案
1、\(\left[-\dfrac 12,4-2\sqrt 2\right]\)
提示 分离变量．
2、\(0\)
提示 \(a^3+b^3+c^3-3abc=(a+b+c)\left(a^2+b^2+c^2-ab-bc-ca\right)\)，于是\(abc=0\)．
3、略
提示 可以两次裂项求和，也可以用数学归纳法．
4、\(\dfrac{7\sqrt 7}4\)
提示 面积最大时，上底长为\(3\)，设底角为\(x\)，面积为\(3\sqrt 2\sin x+\sin 2x\)，利用导数可得当\(\cos x=\dfrac{\sqrt 2}4\)时面积最大．
5、\(-\dfrac 34,-\dfrac 12,-\dfrac 13,1\)
提示 显然\(\dfrac{x^2+4x-1}{7x^2-6x-5}\neq 0\)，于是\[\left|x^2+4x-1\right|\geqslant\left|7x^2-6x-5\right|,\]解得\[-\dfrac 34\leqslant x\leqslant -\dfrac 13\lor 1\leqslant x\leqslant 2.\] 
考虑到\(\dfrac{1-x}{1+x}\)为整数，于是 \(x=\dfrac 2k-1\)，其中\(k\in\mathcal Z\)．于是\(x\)的所有可能的值为\[1,0,-\dfrac 13,-\dfrac 12,-\dfrac 35,-\dfrac 23,-\dfrac 57,-\dfrac 34,\]逐一验证即得．
6、\(A=100^\circ\)
提示 在线段\(BC\)上截取\(BE=BD\)，过\(D\)作\(BC\)的平行线交\(AB\)于\(F\)，则\(\triangle ADF\)与\(\triangle ECD\)全等，进而可求得\(A=100^\circ\)． 
7、略
提示 设方程的根为\(x_1,x_2,x_3\)，则\[7ab-2a^3-9c=\sum_{cyc}{\left(x_1+x_2\right)\left(x_1-x_2\right)^2}\geqslant 0,\]等号当且仅当\(x_1=x_2=x_3\)．