2015年高考数学新课标I卷（理科）压轴题

2015年高考数学新课标I卷（理科）压轴题（第21题）：

已知函数\(f(x)=x^3+ax+\dfrac 14\),\(g(x)=-\ln x\)．

（1）当\(a\)为何值时，\(x\)轴为曲线\(y=f(x)\)的切线；

（2）用\(\min\{m,n\}\)表示\(m,n\)中的最小值，设函数\(h(x)=\min\left\{f(x),g(x)\right\}(x>0)\)，讨论\(h(x)\)零点的个数．

解    （1）根据已知，\(f'(x)=3x^2+a\)．若\(x\)轴为曲线\(y=f(x)\)的切线，设切点横坐标为\(t\)，则有\[\begin{cases}f(t)=0,\\f'(t)=0,\end{cases}\]即\[\begin{cases}t^3+at+\dfrac 14=0,\\3t^2+a=0,\end{cases}\]解得\[t=\dfrac 12,a=-\dfrac 34.\]所以当\(a\)的值为\(-\dfrac 34\)时，\(x\)轴为曲线\(y=f(x)\)的切线．

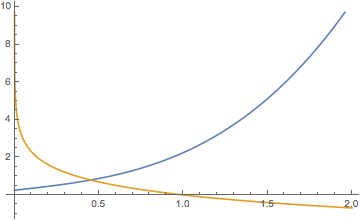
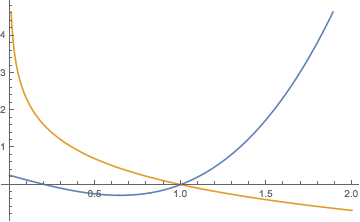
（2）情形一    当\(a\geqslant 0\)时，\(f'(x)=3x^2+a>0\)，于是\(f(x)\)单调递增．考虑到\(f(0)=\dfrac 14>0\)，于是\(y=f(x)\)与\(y=g(x)\)有唯一交点，且交点横坐标\(p\in (0,1)\)，如图．此时函数\(h(x)\)的零点个数为\(1\)．

情形二    当\(-\dfrac 34<a<0\)时，\(f(x)\)在\(\left(0,\sqrt{\dfrac{-a}{3}}\right)\)上单调递减，在\(\left(\sqrt{\dfrac{-a}{3}},+\infty\right)\)上单调递增，在极小值点\(x=\sqrt{\dfrac{-a}{3}}\)处的极小值\[f\left(\sqrt{\dfrac{-a}{3}}\right)=\left(\sqrt{\dfrac{-a}{3}}\right)^3+a\cdot\sqrt{\dfrac{-a}{3}}+\dfrac 14=2\left[\dfrac 18-\left(\sqrt{\dfrac{-a}{3}}\right)^3\right]>0,\]此时\(y=f(x)\)与\(y=g(x)\)在\((0,1)\)内有唯一交点，如图．此时函数\(h(x)\)的零点个数为\(1\)．

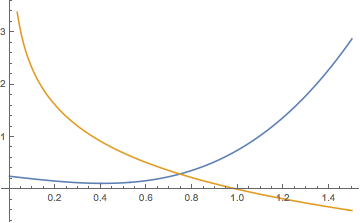
情形三    当\(a=-\dfrac 34\)时，与情形二类似，但此时极小值为\(0\)，如图．此时函数\(h(x)\)的零点个数为\(2\)．

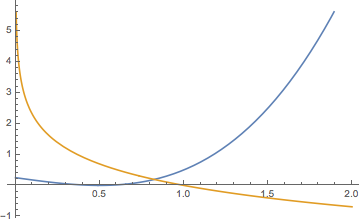
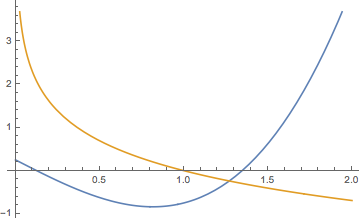
情形四    当\(-\dfrac 54<a<-\dfrac 34\)时，与情形三类似，但此时极小值小于\(0\)，如图．此时函数\(h(x)\)的零点个数为\(3\)．

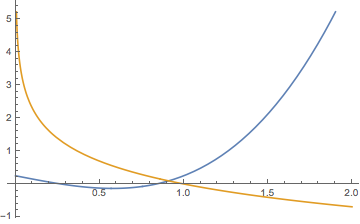
情形五    当\(a=-\dfrac 54\)时，与情形四类似，但此时\(y=f(x)\)与\(y=g(x)\)图象交于点\((1,0)\)，如图．此时函数\(h(x)\)的零点个数为\(2\)．

情形六    当\(a<-\dfrac 54\)时，与情形五类似，但此时\(y=f(x)\)与\(y=g(x)\)图象交点横坐标大于\(1\)，如图．此时函数\(h(x)\)的零点个数为\(1\)．

综上，函数\(h(x)\)的零点个数为\[\begin{cases}1,&a<-\dfrac 54\lor a>-\dfrac 34,\\2,&a=-\dfrac 54 \lor a=-\dfrac 34,\\3,&-\dfrac 54<a<-\dfrac 43.\end{cases}\]