2011年高考福建卷理科数学第10题(选择压轴题):
已知函数\(f(x)={\mathrm e}^x+x\),对于曲线\(y=f(x)\)上横坐标成等差数列的三个点\(A\)、\(B\)、\(C\),给出以下判断:
① 三角形\(ABC\)一定是钝角三角形;
② 三角形\(ABC\)可能是直角三角形;
③ 三角形\(ABC\)可能是等腰三角形;
④ 三角形\(ABC\)不可能是等腰三角形.
其中,正确的判断是( )
A.①③
B.①④
C.②③
D.②④
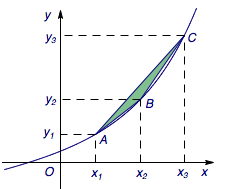
考虑函数\[f'(x)={\mathrm e}^x+1,f'^\prime (x)={\mathrm e}^x,\]因此函数的草图如图.因为在定义域\(\mathcal R\)上,\(f'(x)>0\),于是\(f(x)\)单调递增,有\[y_1<y_2<y_3,\]于是三角形\(ABC\)中,边\(AB\)和边\(BC\)所在的直线的斜率均为正值,于是角\(B\)的外角一定为锐角,进而三角形\(ABC\)一定为钝角三角形.
接下来,在三角形\(ABC\)一定为钝角三角形的前提下,若该三角形为等腰三角形则一定以\(AB\)、\(BC\)为腰.由于在定义域\(\mathcal R\)上,\(f'^\prime (x)>0\),于是\(f'(x)\)单调递增,进而不难得到\[\begin{split}y_2-y_1&=\int_{x_1}^{x_2}{f'(x)}{\mathrm d}x\\&<\left(x_2-x_1\right)f'(x_2)\\&<\int_{x_2}^{x_3}{f'(x)}{\mathrm d}x\\&=y_3-y_2,\end{split}\]因此\[\begin{split}AB&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\\&<\sqrt{\left(x_3-x_2\right)^2+\left(y_3-y_2\right)^2}\\&=BC,\end{split}\]因此三角形\(ABC\)一定不可能是等腰三角形.
综上,①④正确,选B.
补充解法(2016.8.30)
设直线$AB,BC$的斜率分别为$k_{AB},k_{BC}$.
由于函数$f(x)$单调递增,于是$k_{AB},k_{BC}>0$,因此直线$AB$和直线$BC$的倾斜角之差为锐角,进而$\angle ABC$为钝角,命题①正确,命题②错误.
由于$\triangle ABC$为钝角三角形,因此如果它是等腰三角形,那么一定有$AB=BC$,从而$$\sqrt{1+k_{AB}^2}\cdot |x_A-x_B|=\sqrt{1+k_{BC}^2}\cdot |x_B-x_C|,$$结合$k_{AB},k_{BC}>0$,有$k_{AB}=k_{BC}$,进而$A,B,C$三点共线,矛盾.因此$\triangle ABC$不可能为等腰三角形.因此命题③错误,命题④正确.
综上所述,正确的判断是①④.