关于自然对数的底e的两个惊奇事实

一、e的神奇近似        

        刚才看到这个很漂亮的无理数$\rm e$的近似表达，它恰好用到了 1 到 9 这 9 个数字：

$$\rm e\approx\left(1+9^{-4^{7\times 6}}\right)^{3^{2^{85}}}.$$ 猜猜看它能精确到 e 的小数点后多少位？ 10 位？ 100 位？ 1000 位？ 10000 位？

      远比想象中的牛 B —— 它能精确到小数点后 18, 457, 734, 525, 360, 901, 453, 873, 570 位！显然，这绝对不是一个巧合．它的秘密就在于， 事实上

$${\rm e} = \lim_{n\to \infty}\left(1+\dfrac 1n\right)^n,$$ 而 $$9^{4^{7\times 6}}=3^{2^{85}}.$$ 这个指数相当大， Mathematica 直接就报 Overflow 了，难怪它能精确到$\rm e$的小数点后那么多位．

据说，这个神一般的近似表达最早来源于http://www2.stetson.edu/~efriedma/mathmagic/0804.html．并且这个神奇的网页上给出了大量从$1$到$n$的常数近似表达．

---

 

二、杨辉三角中的e

        你相信吗，杨辉三角里竟然也有自然底数 e 的身影．2012 年，Harlan Brothers 发现了杨辉三角中的一个有趣的事实．不妨把杨辉三角第$n$行的所有数之积记作$S_n$，那么随着$n$的增加，$\dfrac {S_n\cdot S_{n+2}}{S_{n+1}^2}$会越来越接近$\rm {e}\approx 2.718$．

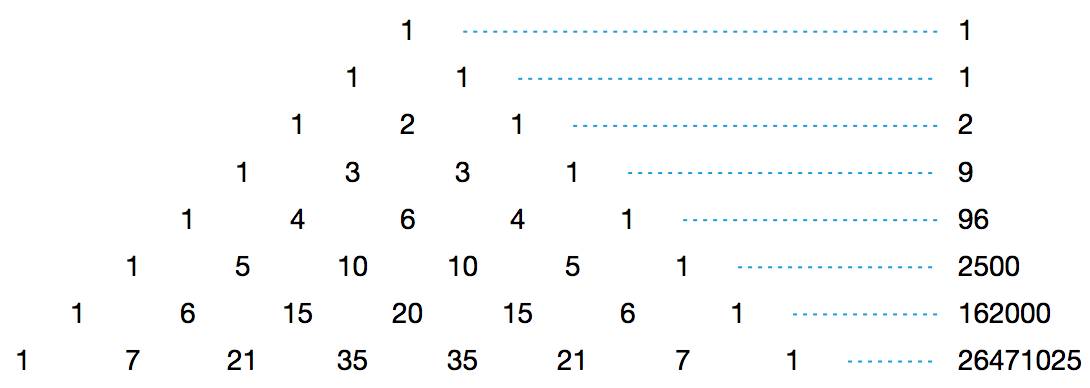
事实上，我们有

$$\lim_{n \to \infty}\dfrac {S_n\cdot S_{n+2}}{S_{n+1}^2}={\rm e}.$$

这是为什么呢？ John Baez 在http://johncarlosbaez.wordpress.com/2014/02/12/triangular-numbers/上给出了一个漂亮的解释．

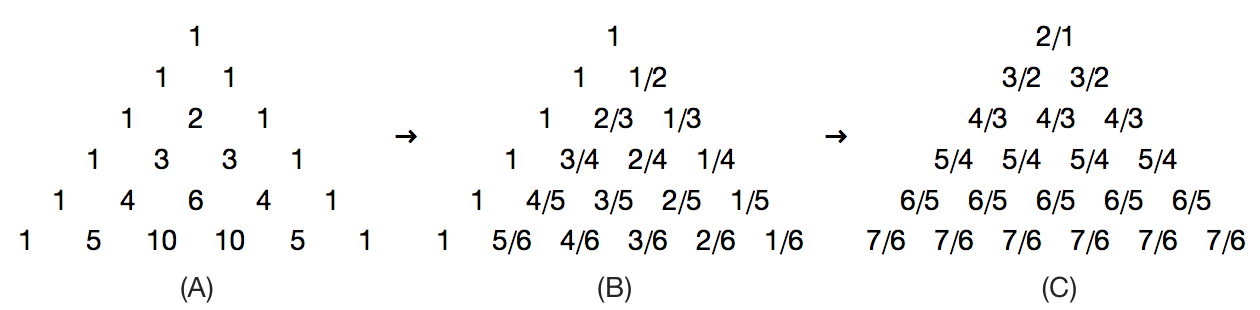
首先，让杨辉三角 (A) 里面的每个数都除以它左下角的那个数，于是得到了图 (B) 所示的三角形数阵．你会发现，这个数阵里有一个很明显的模式，即第$n$行的所有数分母都是$n$，分子则分别是$n, n-1, \cdots, 2, 1$，这并不是巧合．这是因为

$$\dfrac {{\rm C}_m^k}{{\rm C}_{m+1}^k}=\dfrac {\dfrac {m!}{k!(m-k)!}}{\dfrac {(m+1)!}{k!(m-k+1)!}}=\dfrac {m-k+1}{m+1}.$$

接下来，让图 (B) 里的所有数都除以它右下角的那个数，于是得到了图 (C) 所示的三角形数阵．容易看出，这个数阵第$n$行的所有$n$个数应该都是

$$\dfrac {n+1}{n}=1+\dfrac 1n,$$ 它们乘起来等于 $$\left(1+\dfrac 1n\right)^n.$$ 随着$n$的增加，这个数会越来越接近 $\rm e$．

最后，让我们追溯一下图 (C) 中每个数的来源．图 (C) 中$n$行的每个数都等于图 (B) 中第$n$行的某个数除以第$n+1$行的某个数，进而等于图 (A) 中第$n$行的某个数除以第$n+1$行的某个数的结果，除以第$n+1$行的某个数除以第$n+2$行的某个数的结果．因此，图 (C) 中第$n$行的所有数乘起来，结果正是

$$\dfrac {S_n\cdot S_{n+2}}{S_{n+1}^2}.$$

---

2015年1月21日补记：

两段文字均出自Matrix67的博客：

http://www.matrix67.com/blog/archives/3265

http://www.matrix67.com/blog/archives/5881