抛物线的三条切线所围成的三角形称为切线三角形,对应的三个切点形成的三角形称为切点三角形,它们有很多美妙的性质.
1、切线三角形的外接圆过抛物线的焦点.
设抛物线的方程为\(E:x^2=2py\),\(A\left(2pa,2pa^2\right)\),\(B\left(2pb,2pb^2\right)\),\(C\left(2pc,2pc^2\right)\),则三条切线的方程分别为\[\begin{split}B'C'&:2ax-y-2pa^2=0,\\C'A'&:2bx-y-2pb^2=0,\\A'B'&:2cx-y-2pc^2=0,\end{split}\]进而可联立解得\[A'\left(p(b+c),2pbc\right),B'\left(p(c+a),2pca\right),C'\left(p(a+b),2pab\right).\]
因此,三角形\(A'B'C'\)外接二次曲线的方程为\[L_AL_B+\lambda L_BL_C+\mu L_CL_A=0,\]其中\(L_A\)、\(L_B\)、\(L_C\)分别为\(A\)、\(B\)、\(C\)处切线方程的左侧代数式.将其整理为\[Ax^2+By^2+Cxy+Dx+Ey+F=0\]的形式,其中\[\begin{split}A&=4(ab+\lambda bc+\mu ca),\\B&=1+\lambda+\mu,\\C&=-2\left[(a+b)+\lambda (b+c)+\mu (c+a)\right],\end{split}\]为了使得该方程表示圆,有\[A=B\land B=0,\]从而解得\[\begin{cases}\lambda=\dfrac{\left(1+4a^2\right)\left(b-c\right)}{\left(1+4c^2\right)\left(a-b\right)},\\\mu=\dfrac{\left(1+4b^2\right)\left(c-a\right)}{\left(1+4c^2\right)\left(a-b\right)},\end{cases}\]于是三角形\(A'B'C'\)外接圆的方程为\[\sum_{cyc}\left[\left(1+4c^2\right)\left(a-b\right)\left(2ax-2pa^2\right)\left(2bx-y-2pb^2\right)\right]=0,\]将抛物线的焦点坐标\(F\left(0,\dfrac{p}{2}\right)\)代入左边,有\[\begin{split}&\quad \sum_{cyc}\left[\left(1+4c^2\right)\left(a-b\right)\left(-\dfrac p2-2pa^2\right)\left(-\dfrac p2-2pb^2\right)\right]\\&=\dfrac{p^2}{4}\left(1+4a^2\right)\left(1+4b^2\right)\left(1+4c^2\right)\sum_{cyc}\left(a-b\right)\\&=0,\end{split}\]因此性质1得证.
2、切线三角形的垂心在抛物线的准线上.
根据之前的结果,有\[\begin{split}A'H&:y-2pbc=-\dfrac{1}{2a}\left[x-p(b+c)\right],\\B'H&:y-2pca=-\dfrac{1}{2b}\left[x-p(c+a)\right],\end{split}\]从而可得垂心\(H\)的纵坐标满足\[2a(y-2pbc)-2b(y-2pca)=p(b+c)-p(c+a),\]即\[y=-\dfrac{p}{2},\]因此性质2得证.
3、切线三角形的面积是切点三角形面积的一半.
根据之前的结果,有\[\begin{split}S_{\triangle ABC}&=\dfrac 12\begin{vmatrix}1&1&1\\2pa&2pb&2pc\\2pa^2&2pb^2&2pc^2\end{vmatrix}\\&=2p^2\left|(a-b)(b-c)(c-a)\right|,\end{split}\]而\[\begin{split}S_{\triangle A'B'C'}&=\dfrac 12\begin{vmatrix}1&1&1\\p(b+c)&p(c+a)&p(a+b)\\2pbc&2pca&2pab\end{vmatrix}\\&=p^2\left|(a-b)(b-c)(c-a)\right|,\end{split}\]因此性质3得证.
4、抛物线的焦点到切线三角形三个顶点的距离之积与到切点三角形三个顶点的距离之积相等.
根据之前的结果,有\[\begin{split}FA^2\cdot FB^2\cdot FC^2&=\prod_{cyc}\left[\left(2pa\right)^2+\left(\dfrac{p}{2}-2pa^2\right)^2\right]\\&=p^2\prod_{cyc}\left(2a^2+\dfrac{1}{2}\right)^2,\end{split}\]而\[\begin{split}FA'^2\cdot FB'^2\cdot FC'^2&=\prod_{cyc}\left[\left(p(b+c)\right)^2+\left(\dfrac{p}{2}-2pbc\right)^2\right]\\&=p^2\prod_{cyc}\left[\left(2b^2+\dfrac 12\right)\left(2c^2+\dfrac 12\right)\right],\end{split}\]因此性质4得证.
5、对切点三角形而言,可以视切线三角形为割线应用“Menelaus定理”.
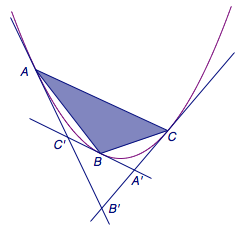 即在图中有\(\dfrac{AB'}{B'C}\cdot\dfrac{CA'}{B'B}\cdot\dfrac{BC'}{C'A}=1\).
即在图中有\(\dfrac{AB'}{B'C}\cdot\dfrac{CA'}{B'B}\cdot\dfrac{BC'}{C'A}=1\).
先证明
引理 过点\(P(x_0,y_0)\)作二次曲线\[Ax^2+By^2+Dx+Ey+F=0\]的割线\(PMN:y=kx+m\),其中\(M\)、\(N\)在二次曲线上,那么\[PM\cdot PN=\left(1+k^2\right)\cdot\left|\dfrac{Ax_0^2+By_0^2+Dx_0+Ey_0+F}{A+Bk^2}\right|.\]
从而可以得到切线长的计算公式,进而可以推得更一般的结论(对一般圆锥曲线均成立),此处从略.

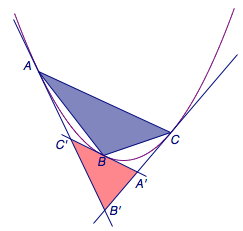


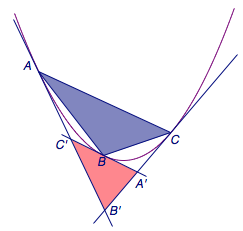

Pingback引用通告: 贝塞尔曲线真的有那么丝滑吗?用事实来一探究竟 – Python量化投资
「性质 5」左式第二项的分母似乎不应为 B'B 而应该是 A'B?
第二个性质利用抛物线的焦点性质结合西姆松线可以得到纯几何解法,攻克第三四条性质ing(๑`・ᴗ・´๑)
第一个性质由光学性质即证,加强版即为您后来发的椭圆旁切焦点张定角,我在圆锥曲线吧也发了一道抛物线的自编题为该性质的加深特例٩( 'ω' )و