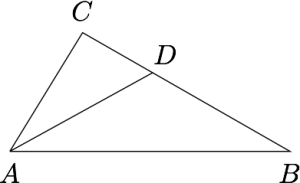
在$\triangle ABC$中,$AB = 2AC$,$AD$是$A$的角平分线,且$AD = kAC$.
(1) 求$k$的取值范围;
(2) 若${S_{\triangle ABC}} = 1$,问$k$为何值时,$BC$最短?
分析与解 (1)不妨设$\angle CAB = 2\theta $,则由$${S_{\triangle ABD}} + {S_{\triangle ACD}} = {S_{\triangle ABC}},$$得$$\dfrac{1}{2}\sin \theta \cdot AB \cdot AD + \dfrac{1}{2}\sin \theta \cdot AC \cdot AD = \dfrac{1}{2}\sin 2\theta \cdot AB \cdot AC,$$于是$$\left( {AB + AC} \right) \cdot AD = 2\cos \theta \cdot AB \cdot AC,$$所以$k = \dfrac{4}{3}\cos \theta \in \left( {0,\dfrac{4}{3}} \right)$.
(2)由$${S_{\triangle ABC}} = \dfrac{1}{2} \cdot 2AC \cdot AC \cdot \sin 2\theta = A{C^2} \cdot \sin 2\theta, $$得$A{C^2} = \dfrac{1}{{\sin 2\theta }}$ .于是\[\begin{split}B{C^2} &= A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos 2\theta \\& = \left( {5 - 4\cos 2\theta } \right) \cdot A{C^2}\\& = \dfrac{{5 - 4\cos 2\theta }}{{\sin 2\theta }}.\end{split}\]令$y = \dfrac{{5 - 4\cos 2\theta }}{{\sin 2\theta }}$,则$y\sin 2\theta + 4\cos 2\theta = 5$,从而有$$\sin \left( {2\theta +\varphi } \right)=\dfrac{5}{{\sqrt {{y^2} + 16} }} \leqslant 1,$$解得$y \geqslant 3$,于是$BC \geqslant \sqrt 3 $.
当$\tan 2\theta = \dfrac{3}{4}$时取到等号,此时$\cos 2\theta = \dfrac{4}{5}$,于是$\cos \theta = \dfrac{3}{{\sqrt {10} }}$,$k = \dfrac{4}{3}\cos \theta = \dfrac{{2\sqrt {10} }}{5}$.