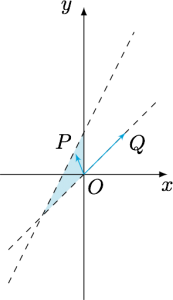
已知$P(x,y)$的坐标满足$\begin{cases}x\leqslant 0,\\ y>x,\\y<2x+1,\end{cases}$求$\dfrac{x+y}{\sqrt{x^2+y^2}}$的取值范围.
正确答案是$\left(-\sqrt 2,1\right]$.
分析与解 根据题意,设$Q(1,1)$,则所求代数式\[m=\dfrac{x+y}{\sqrt{x^2+y^2}}=\sqrt 2\cdot \dfrac{(x,y)\cdot (1,1)}{\sqrt{x^2+y^2}\cdot \sqrt{1^2+1^2}}=\sqrt 2\cos \langle \overrightarrow {OP},\overrightarrow {OQ}\rangle.\]而$\langle \overrightarrow {OP},\overrightarrow {OQ}\rangle$的取值范围是$\left[\dfrac{\pi}4,\pi\right)$,因此$m$的取值范围是$\left(-\sqrt 2,1\right]$.