已知直线$l:x=t$与椭圆$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)相交于$A,B$两点，$M$是椭圆$C$上一点，设直线$MA,MB$分别与$x$轴交于$E,F$两点，$O$为坐标原点，求证：$|OE|\cdot |OF|$为定值．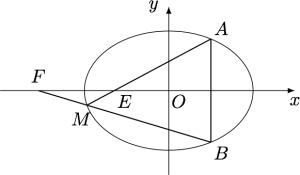
分析与解 法一 坐标法
设$A(t,s)$，$B(t,-s)$，$M(m,n)$，则\[\dfrac{t^2}{a^2}+\dfrac{s^2}{b^2}=\dfrac{m^2}{a^2}+\dfrac{n^2}{b^2}=1,\]且\[|OE|\cdot |OF|=\left|\dfrac{tn-ms}{n-s}\cdot \dfrac{tn-m(-s)}{n-(-s)}\right|=\left|\dfrac{t^2n^2-m^2s^2}{n^2-s^2}\right|,\]将$t^2=a^2-\dfrac{a^2}{b^2}s^2$，$m^2=a^2-\dfrac{a^2}{b^2}n^2$代入，可得$|OE|\cdot |OF|=a^2$为定值．
法二 仿射变换
利用仿射变换$x'=x$，$y'=\dfrac ab y$将椭圆$C$变为圆$C':x'^2+y'^2=a^2$，如图．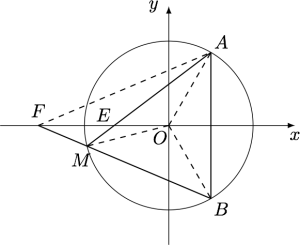
由于$\angle OMB=\angle OBM=\angle OAF$，于是$O,M,F,A$四点共圆，进而有\[\angle OMA=\angle AFO=\angle MFO,\]因此$\triangle OME$与$\triangle OFM$相似，进而\[|OE|\cdot |OF|=|OM|^2=a^2\]为定值．
注 特别的，对$\triangle MAB$应用梅涅劳斯定理，可得$\dfrac{ME}{EA}=\dfrac{MF}{FB}$．