已知不等式$\ln (x+1)-1\leqslant ax+b$对一切$x>-1$都成立，则$\dfrac{b}a$的最小值是_______．
正确答案是$1-{\rm e}$．
分析与解 考虑不等式两边分别对应有函数$f(x)=\ln (x+1)-1$与$g(x)=ax+b$，其中$g(x)$的图象是一条直线，且横截距为$-\dfrac ba$，所以求出当函数$f(x)$的图象在直线$g(x)$下方（或$g(x)$上）时，直线的横截距的最大值即可．
函数$f(x)$的图象如下：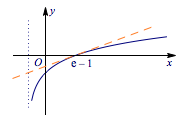
容易看出横截距的最大值为${\rm e}-1$，所以$\dfrac ba$的最小值为$1-{\rm e}$．
注 严格的书写可以在不等式中令$x={\rm e}-1$，于是题中不等式为$$a\left({\rm e}-1+\dfrac ba\right)\geqslant 0,$$不等式恒成立必有$a>0$，从而得到$\dfrac ba\geqslant 1-{\rm e}$，再去验证当$\dfrac ba=1-{\rm e}$时，不等式恒成立．
也可以直接取$f(x)$在$x={\rm e}-1$处的切线，结合对数函数的凹凸性知$$\ln(x+1)-1\leqslant [\ln(x+1)-1]'|_{x={\rm e}-1}\cdot\big(x-({\rm e}-1)\big)=\dfrac 1{\rm e}(x-{\rm e}+1).$$等号在$x={\rm e}-1$时可取到，从而得到$\dfrac ba$的最小值为$1-{\rm e}$．