每日一题[714]各就各“位”

点$M$是棱长为$2$的正方体$ABCD-A_1B_1C_1D_1$的棱切球上的一点，点$N$是$\triangle ACB_1$的外接圆上的一点，则线段$MN$的取值范围是_______．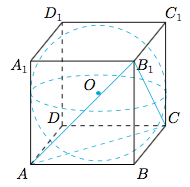

分析与解　记棱切球的球心为$O$，即为正方体的中心，容易求得棱切球的半径为$\sqrt 2$．

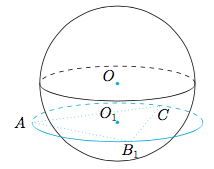
因为$\triangle AB_1C$为正三角形，记它的外接圆圆心为$O_1$，则球心$O$到$\triangle ACB_1$的外接圆上任意一点的距离均为$\sqrt 3$，圆$O_1$与球$O$的位置关系如图：

于是有$OM=\sqrt 2,ON=\sqrt 3$，$M$在球$O$的球面上运动，点$N$在圆$O_1$上运动．因为 $$|ON-OM|\leqslant MN\leqslant OM+ON,$$ 所以线段$MN$的取值范围是$\left[\sqrt 3-\sqrt 2,\sqrt 3+\sqrt 2\right]$，当$M,O,N$三点共线，且$M,N$在$O$的同侧时取到最小值，$M,N$在$O$的异侧时取到最大值．