已知椭圆$E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)所在平面内有一个不与原点重合的点$P(x_0,y_0)$,过$P$作$E$的任意两条割线$AB,CD$,其中$A,B,C,D$均在椭圆$E$上.证明:直线$AC$和$BD$的交点在定直线上.
分析与解 如图,设直线$AC$与$BD$的交点为$Q$,直线$AD$与$BC$的交点为$R$,则直线$RQ$即题中的定直线.
法一 几何方法
如图,设直线$AB,CD$分别与直线$RQ$相交于$S,T$,则利用完全四边形$ABCD$可得四点$S,R,T,Q$为共线的调和点列.下面证明直线$SRTQ$由$P$点位置确定,与直线$AB$和$CD$的作法无关.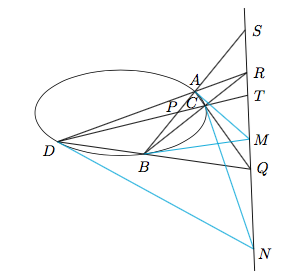 在$A,B$处作切线,两条切线交于$M$;在$C,D$处作切线,两条切线交于$N$.根据帕斯卡(Pascal)定理,$M,N$均在直线$ST$上,即$S,R,T,Q,M,N$六点共线.但从图中可以看出,$S,M$两点只和直线$AB$有关,与直线$CD$完全无关,所以我们将直线$AB$换成任意的另一条直线$A'B'$,只要$A'B'$通过点$P$,则形成的$S,Q,T,Q$四点仍与$M,N$共线.类似的,可以证明直线$SRTQ$的位置与直线$AB$完全无关,而只取决于$P$点位置,因此原命题得证.
在$A,B$处作切线,两条切线交于$M$;在$C,D$处作切线,两条切线交于$N$.根据帕斯卡(Pascal)定理,$M,N$均在直线$ST$上,即$S,R,T,Q,M,N$六点共线.但从图中可以看出,$S,M$两点只和直线$AB$有关,与直线$CD$完全无关,所以我们将直线$AB$换成任意的另一条直线$A'B'$,只要$A'B'$通过点$P$,则形成的$S,Q,T,Q$四点仍与$M,N$共线.类似的,可以证明直线$SRTQ$的位置与直线$AB$完全无关,而只取决于$P$点位置,因此原命题得证.
注 帕斯卡(Pascal)定理:如果一个四边形内接于某圆锥曲线,则四边形的两组对边的两个交点与两组对顶点的切线的两个交点四点共线.
法二 混合方法
首先给出引理.
引理 过点$P$的直线$l$与椭圆交于$S,T$两点,$X$为直线$ST$上的点,那么$P,X$调和分割$S,T$,即“$\dfrac{|SX|}{|XT|}=\dfrac{|SP|}{|PT|}$
”与“点$X$在直线$\dfrac{x_0x}{a^2}+\dfrac{y_0y}{b^2}=1$上”等价.
该引理利用直线的参数方程或定比点差法容易证明,此处从略.
根据引理,我们只需要证明调和分割$A,B$的点以及调和分割$C,D$的点在直线$RQ$上即可(完全四边形的性质).设$AB,CD$与直线$RQ$的交点分别为$S,T$.事实上,对$\triangle CDQ$和截线$APB$应用梅涅劳斯定理,有$$\dfrac{|DB|}{|BQ|}\cdot \dfrac{|QA|}{|AC|}\cdot \dfrac{|CP|}{|PD|}=1,$$对于$\triangle CDQ$和点$R$应用塞瓦定理,有$$\dfrac{|DB|}{|BQ|}\cdot \dfrac{|QA|}{|AC|}\cdot \dfrac{|CT|}{|TD|}=1,$$于是$\dfrac{|CP|}{|PD|}=\dfrac{|CT|}{|TD|}$,因此$P,T$调和分割$C,D$.类似的,有$P,S$调和分割$A,B$.因此原命题得证.
法三 解析方法
设$AB$与$CD$,$AC$与$BD$的交点分别为$P(x_0,y_0)$,$Q(x_1,y_1)$,只需要证明$\dfrac{x_0x_1}{a^2}+\dfrac{y_0y_1}{b^2}=1$即可.设$A\left(a\cos\alpha,b\sin\alpha\right)$,$B\left(a\cos\beta,b\sin\beta\right)$,$C\left(a\cos\gamma,b\sin\gamma\right)$,$D\left(a\cos\delta,b\sin\delta\right)$,则\[\begin{split} &AB:\dfrac xa\cdot \cos\dfrac{\alpha+\beta}2+\dfrac yb\cdot \sin\dfrac{\alpha+\beta}2=\cos\dfrac{\alpha-\beta}2,\\ &CD:\dfrac xa\cdot \cos\dfrac{\gamma+\delta}2+\dfrac yb\cdot \sin\dfrac{\gamma+\delta}2=\cos\dfrac{\gamma-\delta}2,\end{split} \]于是直线$AB$与$CD$的交点坐标为$$\left(a\cdot \dfrac{\cos\dfrac{\alpha-\beta}2\sin\dfrac{\gamma+\delta}2-\sin\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2}{\cos\dfrac{\alpha+\beta}2\sin\dfrac{\gamma+\delta}2-\sin\dfrac{\alpha+\beta}2\cos\dfrac{\gamma+\delta}2},b\cdot \dfrac{\cos\dfrac{\alpha-\beta}2\cos\dfrac{\gamma+\delta}2-\cos\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2}{\sin\dfrac{\alpha+\beta}2\cos\dfrac{\gamma+\delta}2-\cos\dfrac{\alpha+\beta}2\sin\dfrac{\gamma+\delta}2}\right)$$即$$\left(a\cdot \dfrac{\sin\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2-\cos\dfrac{\alpha-\beta}2\sin\dfrac{\gamma +\delta}2}{\sin\dfrac{\alpha+\beta-\gamma-\delta}2},b\cdot\dfrac{\cos\dfrac{\alpha-\beta}2\cos\dfrac{\gamma+\delta}2-\cos\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2}{\sin\dfrac{\alpha+\beta-\gamma-\delta}2}\right),$$交换$\gamma$和$\beta$就可以得到$AC$与$BD$的交点坐标,为$$\left(a\cdot \dfrac{\sin\dfrac{\alpha+\gamma}2\cos\dfrac{\beta-\delta}2-\cos\dfrac{\alpha-\gamma}2\sin\dfrac{\beta +\delta}2}{\sin\dfrac{\alpha+\gamma-\beta-\delta}2},b\cdot\dfrac{\cos\dfrac{\alpha-\gamma}2\cos\dfrac{\beta+\delta}2-\cos\dfrac{\alpha+\gamma}2\cos\dfrac{\beta-\delta}2}{\sin\dfrac{\alpha+\gamma-\beta-\delta}2}\right).$$于是我们只需证明\[\begin{split}& \left(\sin\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2-\cos\dfrac{\alpha-\beta}2\sin\dfrac{\gamma +\delta}2\right)\cdot\left(\sin\dfrac{\alpha+\gamma}2\cos\dfrac{\beta-\delta}2-\cos\dfrac{\alpha-\gamma}2\sin\dfrac{\beta +\delta}2\right) \\ &\qquad\qquad +\left(\cos\dfrac{\alpha-\beta}2\cos\dfrac{\gamma+\delta}2-\cos\dfrac{\alpha+\beta}2\cos\dfrac{\gamma-\delta}2\right)\cdot \left(\cos\dfrac{\alpha-\gamma}2\cos\dfrac{\beta+\delta}2-\cos\dfrac{\alpha+\gamma}2\cos\dfrac{\beta-\delta}2\right)\\ &\qquad\qquad\qquad\qquad\qquad \qquad\qquad \qquad\qquad \qquad\qquad \qquad\qquad =\sin\dfrac{\alpha+\beta-\gamma-\delta}2\cdot \sin\dfrac{\alpha+\gamma-\beta-\delta}2.\end{split} \]事实上,有\[\begin{split} LHS&=\cos\dfrac{\gamma-\delta}2\cos\dfrac{\beta-\delta}2\left(\sin\dfrac{\alpha+\beta}2\sin\dfrac{\alpha+\gamma}2+\cos\dfrac{\alpha+\beta}2\cos\dfrac{\alpha+\gamma}2\right)\\
&\qquad \qquad +\cos\dfrac{\gamma-\delta}2\cos\dfrac{\alpha-\gamma}2\left(-\sin\dfrac{\alpha+\beta}2\sin\dfrac{\beta+\delta}2-\cos\dfrac{\alpha+\beta}2\cos\dfrac{\beta+\delta}2\right)\\
&\qquad \qquad+\cos\dfrac{\alpha-\beta}2\cos\dfrac{\beta-\delta}2\left(-\sin\dfrac {\gamma+\delta}2\sin\dfrac{\alpha+\gamma}2-\cos\dfrac {\gamma+\delta}2\cos\dfrac{\alpha+\gamma}2\right)\\
&\qquad \qquad+\cos\dfrac{\alpha-\beta}2\cos\dfrac{\alpha-\gamma}2\left(\sin\dfrac{\gamma+\delta}2\sin\dfrac{\beta+\delta}2+\cos\dfrac{\gamma+\delta}2\cos\dfrac{\beta+\delta}2\right)\\
&=\cos\dfrac{\gamma-\delta}2\cos\dfrac{\beta-\delta}2\cos\dfrac{\beta-\gamma}2-\cos\dfrac{\gamma-\delta}2\cos\dfrac{\alpha-\gamma}2\cos\dfrac{\alpha-\delta}2\\
&\qquad \qquad-\cos\dfrac{\alpha-\beta}2\cos\dfrac{\beta-\delta}2\cos\dfrac{\alpha-\delta}2+\cos\dfrac{\alpha-\beta}2\cos\dfrac{\alpha-\gamma}2\cos\dfrac{\beta-\gamma}2\\
&=\cos\dfrac{\gamma-\delta }2\cos\left(\dfrac{\alpha-\beta}2+\dfrac{\delta-\alpha}2\right)\cos\dfrac{\beta-\gamma}2-\cos\dfrac{\gamma-\delta}2\cos\left(\dfrac{\alpha-\beta}2+\dfrac{\beta-\gamma}2\right)\cos\dfrac{\delta-\alpha}2\\
&\qquad \qquad-\cos\dfrac{\alpha-\beta}2\cos\left(\dfrac{\beta-\gamma}2+
\dfrac{\gamma-\delta}2\right)\cos\dfrac{\delta-\alpha}2+\cos\dfrac{\alpha-\beta}2\cos\left(\dfrac{\gamma-\delta}2+\dfrac{\delta-\alpha}2\right)\cos\dfrac{\beta-\gamma}2\\
&=\sin\dfrac{\alpha-\beta}2\sin\dfrac{\beta-\gamma}2\cos\dfrac{\gamma-\delta}2\cos\dfrac{\delta-\alpha}2-\sin\dfrac{\alpha-\beta}2\cos\dfrac{\beta-\gamma}2\cos\dfrac{\gamma-\delta}2\sin\dfrac{\delta-\alpha}2\\
&\qquad \qquad+\cos\dfrac{\alpha-\beta}2\sin\dfrac{\beta-\gamma}2\sin\dfrac{\gamma-\delta}2\cos\dfrac{\delta-\alpha}2-\cos\dfrac{\alpha-\beta}2\cos\dfrac{\beta-\gamma}2\sin\dfrac{\gamma-\delta}2\sin\dfrac{\delta-\alpha}2\\
&=\sin\dfrac{\alpha-\beta}2\cos\dfrac{\gamma-\delta}2\left(\sin\dfrac{\beta-\gamma}2\cos\dfrac{\delta-\alpha}2-\cos\dfrac{\beta-\gamma}2\sin\dfrac{\delta -\alpha}2\right)\\
&\qquad \qquad+\cos\dfrac{\alpha-\beta}2\sin\dfrac{\gamma-\delta}2\left(\sin\dfrac{\beta-\gamma}2\cos\dfrac{\delta-\alpha}2-\cos\dfrac{\beta-\gamma}2\sin\dfrac{\delta-\alpha}2\right)\\
&=\sin\dfrac{\alpha-\beta}2\cos\dfrac{\gamma-\delta}2\sin\dfrac{\alpha+\beta-\gamma-\delta}2+\cos\dfrac{\alpha-\beta}2\sin\dfrac{\gamma-\delta}2\sin\dfrac{\alpha+\beta-\gamma-\delta}2\\
&=\sin\dfrac{\alpha-\beta+\gamma-\delta}2\sin\dfrac{\alpha+\beta-\gamma-\delta}2\\
&=RHS,\end{split}\]因此原命题得证.

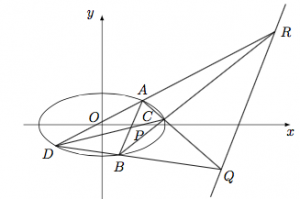
能不能用前面介绍的仿射变换处理?