1．已知函数$f(x)={\log_4}x-\left(\dfrac 14\right)^x$和函数$g(x)={\log_{\frac 14}}x-\left(\dfrac 14\right)^x$的零点分别为$x_1,x_2$，则（ ）
A．$0<x_1x_2<1$
B．$x_1x_2=1$
C．$1<x_1x_2<2$
D．$x_1x_2\geqslant 2$
2．求$\dfrac{2\cos 10^\circ}{\sin 70^\circ}-\tan 20^\circ$的值．
3．已知函数$f(x)$的定义域是$D$，若对于任意$x_1,x_2\in D$，当$x_1<x_2$时，都有$f(x_1)\leqslant f(x_2)$，则称函数$f(x)$为在$D$上的非减函数．设函数$f(x)$在$[0,1]$上是非减函数，且满足以下三个条件：
(1) $f(0)=0$；
(2) $f\left(\dfrac x5\right)=\dfrac 12f(x)$；
(3) $f(1-x)=1-f(x)$．
则$f\left(\dfrac 45\right)=$_____，$f\left(\dfrac{1}{12}\right)=$_____ ，$f\left(\dfrac{1}{2016}\right)=$_____．
4．若$a,b,c$为非零复数，且$\dfrac ab=\dfrac bc=\dfrac ca$，求$\dfrac{a+b+c}{a-b+c}$的值．
5．设复数$z$满足$|z|=1$，求$\left|z^3-3z-2\right|$的取值范围．
6．(2011年广东卷)设$S$是整数集$\mathcal Z$的非空子集，如果$\forall a,b\in S$，$ab\in S$，则称$S$关于数的乘法是封闭的．若$T,V$是$\mathcal Z$的两个不相交的非空子集，$T\cup U=\mathcal Z$，且$\forall a,b,c\in T$，$abc\in T$；$\forall x,y,z\in V$，$xyz\in V$，则下列结论恒成立的是（ ）
A．$T,V$中至少有一个关于乘法是封闭的
B．$T,V$中至多有一个关于乘法是封闭的
C．$T,V$中有且只有一个关于乘法是封闭的
D．$T,V$均关于乘法是封闭的
7．(2012年天津河西区高三期末考试)已知数列$\{a_n\}$满足$a_1=\dfrac 12$，$a_{n+1}=\dfrac{(n+1)(2a_n-n)}{a_n+4n}$($n\in\mathcal N^*$)．
(1) 求$a_2,a_3,a_4$；
(2) 已知存在实数$k$，使得数列$\left\{\dfrac{a_n+k\cdot n}{a_n+n}\right\}$为公差是$-1$的等差数列，求$k$的值；
(3) 记$b_n=\dfrac{1}{3^{\frac {n+2}2}\cdot a_{n+2}}$，数列$\{b_n\}$的前$n$项和为$S_n$，求证：$S_n>-\dfrac{2\sqrt 3+1}{12}$．
参考答案
1．画图配合计算，容易判断出$\dfrac 12=x_2<1<x_1<2$，于是$\dfrac 12<x_1x_2<1$，选A．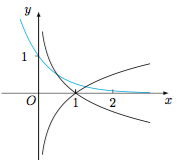
2．根据题意，有\[\begin{split} \dfrac{2\cos 10^\circ}{\sin 70^\circ}-\tan 20^\circ&=\dfrac{2\cos 10^\circ}{\sin 70^\circ}-\dfrac{\sin 20^\circ}{\cos 20^\circ}\\&=\dfrac{2\cos 10^\circ-\sin 20^\circ}{\cos 20^\circ}\\&=\dfrac{2\cos(30^\circ-20^\circ)-\sin 20^\circ}{\cos 20^\circ}\\&=\dfrac{\sqrt 3\cos 20^\circ+\sin 20^\circ-\sin 20^\circ}{\cos 20^\circ}\\
&=\sqrt 3.\end{split} \]
3．由于$f(0)=0$，$f(1)=1$，$f\left(\dfrac 15\right)=f\left(\dfrac 45\right)=\dfrac 12$，因此$f(x)=\dfrac 12$，$x\in\left[\dfrac 15,\dfrac 45\right]$．进而可得$f\left(\dfrac{x}{5^n}\right)=\dfrac{1}{2^n}f(x)$，因此有$$f(x)=\dfrac{1}{2^n},\dfrac{1}{5^n}\leqslant x\leqslant \dfrac{4}{5^n}.$$综上所述，有$f\left(\dfrac 45\right)=\dfrac 12$，$f\left(\dfrac{1}{12}\right)=\dfrac 14$，$f\left(\dfrac{1}{2016}\right)=\dfrac{1}{32}$．
4．令$\dfrac ab=\dfrac bc=\dfrac ca=x$，则$x^3=1$，于是$x=1$或$x=\omega$或$x=\omega^2$，其中$\omega=-\dfrac 12+\dfrac{\sqrt 3}2{\rm i}$．而$$\dfrac{a+b+c}{a-b+c}=\dfrac{\dfrac ab+\dfrac cb+1}{\dfrac ab+\dfrac cb-1}=\dfrac{x+\dfrac 1x}{x+\dfrac 1x-1}=\dfrac {x^2+x+1}{x^2-x+1}.$$
情形一 $x=1$．此时$\dfrac{a+b+c}{a-b+c}=3$．
情形二 $x\neq 1$．此时$x^2+x+1=\dfrac{x^3-1}{x-1}=0$，于是$\dfrac{a+b+c}{a-b+c}=0$.
综上所述，$\dfrac{a+b+c}{a-b+c}$的值为$3$或$0$．
5．法一 三角形式
设$z=\cos\theta+{\rm i}\sin\theta$，则\[\begin{split} \left|z^3-3z-2\right|&=|z+1|^2\cdot |z-2|\\ &=(2+2\cos\theta)\cdot \sqrt{5-4\cos\theta}\\
&=\sqrt{(2+2\cos\theta)(2+2\cos\theta)(5-4\cos\theta)},\end{split} \]由均值不等式易得所求的取值范围是$\left[0,3\sqrt 3\right]$．
法二 共轭复数
设$z+\overline z=t$，$t\in [-2,2]$，则\[\begin{split} \left|z^3-3z-2\right|^2&=\left(z^3-3z-2\right)\cdot\left({\overline z}^3-3\overline z-2\right)\\
&=-2t^3-3t^2+12t+20,\end{split} \]利用导数可以求得所求的取值范围是$\left[0,3\sqrt 3\right]$．
6．将$\mathcal Z$划分为奇数集和偶数集，那么它们关于数的乘法均封闭；将$\mathcal Z$划分为负整数集和非负整数集，那么负整数集不是关于数的乘法封闭的，而非负整数集关于数的乘法封闭．下面我们证明选项A是正确的．考虑到$1$必然在$T$或$U$中，而包含$1$的那个集合必然关于数的乘法是封闭的，因此$T,V$中至少有一个关于乘法是封闭的．
7．(1) 根据题意，有$$\dfrac{a_{n+1}}{n+1}=\dfrac{2\cdot \dfrac{a_n}n-1}{\dfrac{a_n}n+4},$$令$x_n=\dfrac{a_n}n$，可得$$x_{n+1}=\dfrac{2x_n-1}{x_n+4},x_1=\dfrac 12,$$利用不动点改造递推公式，可得$$\dfrac{1}{x_{n+1}+1}=\dfrac{1}{x_n+1}+\dfrac 13,$$因此可得$x_n=\dfrac{3}{n+1}-1$，进而$a_n=\dfrac{n(2-n)}{n+1}$，因此$a_2=0$，$a_3=-\dfrac 34$，$a_4=-\dfrac 85$．
(2) 根据题意，有$$\dfrac{a_n+k\cdot n}{a_n+n}=\dfrac{k-1}3n+\dfrac{k+2}3,$$因此当$k=-2$时，该数列为公差是$-1$的等差数列．
(3) 根据题意，有$$b_n=\dfrac{-n-3}{\left(\sqrt 3\right)^{n+2}\cdot n(n+2)}=\dfrac 12\left[\dfrac{1}{\left(\sqrt 3\right)^{n+2}\cdot(n+2)}-\dfrac{1}{\left(\sqrt 3\right)^n\cdot n}\right],$$于是有$$S_n>\dfrac 12\left(-\dfrac{1}{\sqrt 3}-\dfrac 16\right)=-\dfrac{2\sqrt 3+1}{12}.$$