已知函数$y=\ln x-(ax+b)$有两个不同的零点$x_1,x_2$,求证:$\dfrac{{\rm e}^{1+b}}{a}<x_1x_2<\dfrac{1}{a^2}$.
分析与解 问题等价于$f_1(x)=x-a{\rm e}^x-b$有两个不同的零点$x_1,x_2$,求证:$1+b-\ln a<x_1+x_2<-2\ln a$.尝试使用构造函数的方法证明极值点偏移不等式.
右边不等式 由于$f_1'(x)=1-a{\rm e}^x$,因此$a>0$,其极值点为$x=-\ln a$.又由于函数$f_1(x)$的二阶导函数$f_1''(x)=-a{\rm e}^x$,因此构造函数$$g_1(x)=\dfrac 12f_1''(-\ln a)\cdot(x+\ln a)^2+f_1(-\ln a),$$则$h_1(x)=f_1(x)-g_1(x)$的二阶导函数$$h_1''(x)=f_1''(x)-f_1''(-\ln a)=1-a{\rm e}^x,$$因此在$(-\infty,-\ln a)$上,$h_1''(x)>0$,在$(-\ln a,+\infty)$上,$h_1''(x)<0$;结合$h_1'(-\ln a)=0$,在$\mathbb R$上,$h_1'(x)\leqslant 0$;结合$h_1(-\ln a)=0$,在$(-\infty,-\ln a)$上,$h_1(x)>0$,在$(-\ln a,+\infty)$上,$h_1(x)<0$,如图.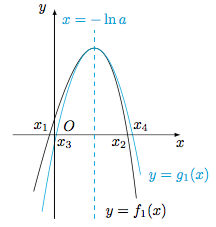 因此二次函数$g_1(x)=\dfrac 12f_1''(-\ln a)\cdot(x+\ln a)^2+f_1(-\ln a)$的零点$x_3,x_4$($x_3<x_4$)满足$$x_1<x_3<x_2<x_4,$$因此$x_1+x_2<x_3+x_4=-2\ln a$.
因此二次函数$g_1(x)=\dfrac 12f_1''(-\ln a)\cdot(x+\ln a)^2+f_1(-\ln a)$的零点$x_3,x_4$($x_3<x_4$)满足$$x_1<x_3<x_2<x_4,$$因此$x_1+x_2<x_3+x_4=-2\ln a$.
左边不等式 此时无法通过构造二次函数证明.设$f_2(x)=\ln x-(ax+b)$,则其导函数$f_2'(x)=\dfrac 1x-a$,因此其极大值点为$x=\dfrac 1a$.欲证明的不等式为$$\ln x_1+\ln x_2>1+b-\ln a,\ \text{即} \ x_1+x_2>\dfrac{1-b-\ln a}a.$$构造函数$$g_2(x)=\dfrac 1{\alpha x+\beta}+\gamma -(ax+b),$$其中$g_2(x)$与$f_2(x)$在$x=\dfrac 1a$处的函数值,导函数值和二阶导函数值均相等,则可以求得$$g_2(x)=-\dfrac{4}{ax+1}+2-\ln a-(ax+b),$$此时$h_2(x)=f_2(x)-g_2(x)$的导函数$$h_2'(x)=\dfrac 1x-\dfrac{4a}{(ax+1)^2}=\dfrac{(ax-1)^2}{x(ax+1)^2}\geqslant 0,$$结合$h_2\left(\dfrac 1a\right)=0$可得$h_2(x)$在$x=\dfrac 1a$的两侧异号,如图.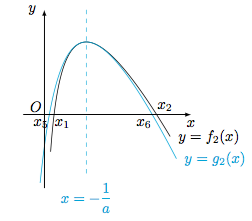 而函数$g_2(x)$的零点$x_5,x_6$($x_5<x_6$)即方程$$\dfrac{-a^2x^2+a(1-\ln a-b)-4}{ax+1}=0$$的两根,有$x_5+x_6=\dfrac{1-b-\ln a}a$,因此$$x_5<x_1<x_6<x_2,$$可得$x_1+x_2>x_5+x_6>\dfrac{1-b-\ln a}a$,原命题得证.
而函数$g_2(x)$的零点$x_5,x_6$($x_5<x_6$)即方程$$\dfrac{-a^2x^2+a(1-\ln a-b)-4}{ax+1}=0$$的两根,有$x_5+x_6=\dfrac{1-b-\ln a}a$,因此$$x_5<x_1<x_6<x_2,$$可得$x_1+x_2>x_5+x_6>\dfrac{1-b-\ln a}a$,原命题得证.
思考与总结 利用导数用一次函数、二次函数、一次分式函数、对勾函数等简单初等函数对复杂函数进行拟合,从而将复杂函数的零点问题转化为简单函数的零点问题.
接来下用A-L-G不等式证明该命题.
由于$\ln x_1=ax_1+b$,$\ln x_2=ax_2+b$,于是$$a=\dfrac{\ln x_1-\ln x_2}{x_1-x_2}<\dfrac{1}{\sqrt{x_1x_2}},$$即$x_1x_2<\dfrac{1}{a^2}$,右侧不等式得证.
另一方面,左侧不等式即$$\ln x_1+\ln x_2>1+b-\ln a,\ \text{也即} \ a(x_1+x_2)>1-b-\ln a.$$由于函数的$y=\ln x-(ax+b)$的极大值点为$x=\dfrac 1a$,因此不妨设$0<x_1<\dfrac 1a<x_2$.由A-L-G不等式可得$$\dfrac{\ln x_1-\ln\dfrac 1a}{x_1-\dfrac 1a}>\dfrac{2}{x_1+\dfrac 1a},\dfrac{\ln x_2-\ln\dfrac 1a}{x_2-\dfrac 1a}>\dfrac{2}{x_2+\dfrac 1a},$$即$$(ax_1+b+\ln a)\left(x_1+\dfrac 1a\right)<2\left(x_1-\dfrac 1a\right),(ax_2+b+\ln a)\left(x_2+\dfrac 1a\right)>2\left(x_2-\dfrac 1a\right),$$两式相减可得$$a(x_1^2-x_2^2)+(b+\ln a+1)(x_1-x_2)<2(x_1-x_2),$$也即$$a(x_1+x_2)+b+\ln a+1>2,$$原命题得证.
最后给出两道练习:
练习一 已知函数$y=\dfrac{\ln x}x-k$有两个零点$x_1,x_2$.求证:$x_1+x_2>2{\rm e}$.进一步,求证:$x_1+x_2>\dfrac{2}{k}$.
证明 不妨设$x_1<x_2$,函数$f(x)=\dfrac{\ln x}x-k$,则其导函数$$f'(x)=\dfrac{1-\ln x}{x^2}.$$因此函数$f(x)$的极大值点为$x={\rm e}$,极大值为$f({\rm e})=\dfrac{1}{\rm e}-k$.于是$k\in\left(0,\dfrac{1}{\rm e}\right)$.
第一个不等式 函数$f(x)$的二阶导函数$$f''(x)=\dfrac{2\ln x-3}{x^3},$$进而构造函数$$h(x)=f(x)-\left[\dfrac 12f''({\rm e})\cdot(x-{\rm e})^2+f({\rm e})\right],$$则其二阶导函数$$h''(x)=f''(x)-f''({\rm e})=\dfrac{2\ln x-3}{x^3}+\dfrac{1}{{\rm e}^3}=\dfrac{2\ln x-3+\dfrac{x^3}{{\rm e}^3}}{x^3},$$于是在$(0,{\rm e})$上$h''(x)<0$,在$({\rm e},+\infty)$上$h''(x)>0$;进而结合$h'({\rm e})=0$,在$(0,+\infty)$上$h'(x)\geqslant 0$;进而结合$h({\rm e})=0$,有$h(x)$在$(0,{\rm e})$上$h(x)<0$,在$({\rm e},+\infty)$上$h(x)>0$,如图.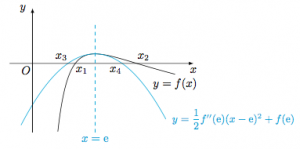 因此有二次函数$y=\dfrac 12f''({\rm e})(x-{\rm e})^2+f({\rm e})$的零点$x_3,x_4$($x_3<x_4$)满足$$x_3<x_1<x_4<x_2,$$从而$x_1+x_2>x_3+x_4=2{\rm e}$,原命题得证.
因此有二次函数$y=\dfrac 12f''({\rm e})(x-{\rm e})^2+f({\rm e})$的零点$x_3,x_4$($x_3<x_4$)满足$$x_3<x_1<x_4<x_2,$$从而$x_1+x_2>x_3+x_4=2{\rm e}$,原命题得证.
第二个不等式 设函数$g(x)=\ln x-kx$,则函数$g(x)$的导函数$$g'(x)=\dfrac{1}{x}-k,$$因此函数$g(x)$的极大值点为$x=\dfrac 1k$,其二阶导函数$$g''(x)=-\dfrac{1}{x^2},$$进而构造函数$$\varphi(x)=g(x)-\left[\dfrac 12g''\left(\dfrac 1k\right)\cdot\left(x-\dfrac 1k\right)^2+g\left(\dfrac 1k\right)\right],$$则其二阶导函数$$\varphi''(x)=g''(x)-g''\left(\dfrac 1k\right)=\dfrac{k^2x^2-1}{x^2},$$于是在$\left(0,\dfrac 1k\right)$上$\varphi''(x)<0$,在$\left(\dfrac 1k,+\infty\right)$上$\varphi''(x)>0$;进而结合$\varphi'\left(\dfrac 1k\right)=0$,在$\left(0,+\infty\right)$上$\varphi'(x)\geqslant 0$;进而结合$\varphi\left(\dfrac 1k\right)=0$,有$\varphi(x)$在$\left(0,+\infty\right)$上$\varphi(x)<0$,在$\left(\dfrac 1k,+\infty\right)$上$\varphi(x)>0$,如图.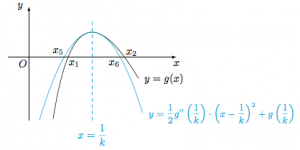 因此有二次函数$y=\dfrac 12g''\left(\dfrac 1k\right)\left(x-\dfrac 1k\right)^2+g\left(\dfrac 1k\right)$的零点$x_5,x_6$($x_5<x_6$)满足$$x_5<x_1<x_6<x_2,$$从而$x_1+x_2>x_5+x_6=\dfrac 2{k}$,原命题得证.
因此有二次函数$y=\dfrac 12g''\left(\dfrac 1k\right)\left(x-\dfrac 1k\right)^2+g\left(\dfrac 1k\right)$的零点$x_5,x_6$($x_5<x_6$)满足$$x_5<x_1<x_6<x_2,$$从而$x_1+x_2>x_5+x_6=\dfrac 2{k}$,原命题得证.
练习二 已知$f(x)={\rm e}^x-x-1$,若$f(x_1)=f(x_2)$,$x_1\neq x_2$,比较$\left({\rm e}^{x_1}-1\right)\left({\rm e}^{x_2}-1\right)$与$x_1x_2$的大小关系.
解 设$f(x_1)=f(x_2)=a$,则$$\left({\rm e}^{x_1}-1\right)\left({\rm e}^{x_2}-1\right)-x_1x_2=(x_1+a)(x_2+a)-x_1x_2=a(x_1+x_2+a).$$我们熟知${\rm e}^x\geqslant x+1$,等号当且仅当$x=0$时取得,因此$a>0$,问题转换为比较$x_1+x_2$与$-a$的大小关系.构造函数$$g(x)=-\dfrac{4}{x-2}-1-x-1,x<2,$$则函数$h(x)=f(x)-g(x)$的导函数$$h'(x)={\rm e}^x-\dfrac{4}{(x-2)^2}=\dfrac{{\rm e}^x(x-2)^2-4}{(x-2)^2},x<2,$$设$r(x)={\rm e}^x(x-2)^2-4$($x<2$),则$$r'(x)={\rm e}^x\cdot x(x-2),$$于是$r(x)$在$x=0$处取得极小值,亦为最小值$r(0)=0$,因此$h'(x)\geqslant 0$;结合$h(0)=0$,在$(-\infty,0)$上有$h(x)<0$,在$(0,1)$上有$h(x)>0$,如图.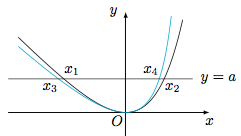 不妨设$x_1<x_2$,方程$g(x)=a$的实数根为$x_3,x_4$($x_3,x_4$),则$x_3<x_1<x_4<x_2$,即$x_1+x_2>x_3+x_4$.而方程$g(x)=a$,也即$$x^2+ax-2a=0,$$因此$x_3+x_4=-a$.这样我们就得到了$x_1+x_2>-a$.
不妨设$x_1<x_2$,方程$g(x)=a$的实数根为$x_3,x_4$($x_3,x_4$),则$x_3<x_1<x_4<x_2$,即$x_1+x_2>x_3+x_4$.而方程$g(x)=a$,也即$$x^2+ax-2a=0,$$因此$x_3+x_4=-a$.这样我们就得到了$x_1+x_2>-a$.
更多的练习:
1、已知方程$\dfrac{(x-1)\ln x}x=m$的两个实数解为$x_1,x_2$,求证:$x_1+x_2>2$.
提示 构造函数$y=(x-1)^2$.
2、已知方程$\dfrac{\ln x+1}{{\rm e}^x}=m$的两个实数解为$x_1,x_2$,求证:$x_1+x_2>2$.
提示 构造函数$-\dfrac{1}{\rm e}(x-1)^2+\dfrac{1}{\rm e}$.

兰老师您好,我的问题也和楼上的评论一样,构造函数的依据或者方法是什么呀?
自己看懂了哈哈,谢谢兰老师做这么好的资料!
兰老师:您好
请问在什么情况下因此构造二次函数y=1/2 f ′′ (e)(x−e) 2 +f(e) ?什么情况下因此构造函数h(x)=f(x)−[1/12 f ′′ (e)⋅(x−e) 2 +f(e)]?