如图,正方形$ABCD$中,$E$为$AB$的中点,$P$为以$A$为圆心的弧$BD$上一点(包含端点),且$\overrightarrow{AC}=\lambda\overrightarrow{DE}+\mu\overrightarrow{AP}$,求$\lambda+\mu$的取值范围.
解 根据题意,有\[\begin{split} \mu \overrightarrow{AP}&=\overrightarrow{AC}-\lambda (\overrightarrow{AE}-\overrightarrow{AD}) \\ &=\overrightarrow{AB}+\overrightarrow{AD}-\dfrac 12\lambda\overrightarrow{AB}+\lambda\overrightarrow{AD}\\ &=\left(1-\dfrac 12\lambda\right)\overrightarrow{AB}+\left(1+\lambda\right)\overrightarrow{AD},\end{split} \]由于$P$在圆弧$BD$上运动,因此$$\left(1-\dfrac 12\lambda\right)\cdot \left(1+\lambda\right)\geqslant 0,$$解得$$-1\leqslant \lambda \leqslant 2,\mu\geqslant 0.$$
于是$$\mu\overrightarrow{AP}\cdot \mu\overrightarrow{AP}=\left[\left(1-\dfrac 12\lambda\right)\overrightarrow{AB}+(1+\lambda)\overrightarrow{AD}\right]\cdot\left[\left(1-\dfrac 12\lambda\right)\overrightarrow{AB}+(1+\lambda)\overrightarrow{AD}\right],$$从而$$\mu^2=\left(1-\dfrac 12\lambda \right)^2+(1+\lambda)^2,$$由$(1+\lambda )^2\geqslant 0,\mu\geqslant 0,1-\dfrac 12\lambda \geqslant 0$得到$$\lambda+\mu\geqslant \lambda+\left(1-\dfrac 12\lambda\right) =1+\dfrac 12\lambda\geqslant \dfrac 12,$$等号当且仅当$\lambda=-1$时取得,而$$\lambda+\mu\leqslant \lambda + \left(1-\dfrac 12\lambda +1+\lambda\right)=2+\dfrac 32\lambda \leqslant 5,$$等号当且仅当$\lambda =2$时取得.
综合连续性,可得$\lambda+\mu$的取值范围是$\left[\dfrac 12,5\right]$.
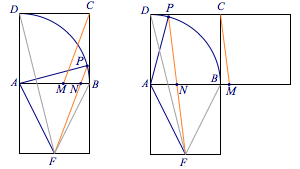
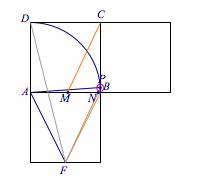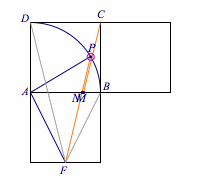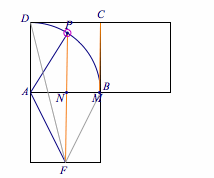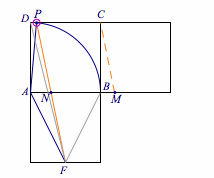
注 本题也可以通过共线向量的系数和关系,直接结合图象得到范围,将正方形$ABCD$往下平移,使得两个正方形恰有一条边重合,如图,记$F$为$E$平移后得到的点,则$\overrightarrow {DE}=\overrightarrow {AF}$,于是$$\overrightarrow {AC}=\lambda \overrightarrow {AF}+\mu\overrightarrow {AP}.$$
连结$PF$,交$AB$于点$N$,过$C$作$PF$的平行线交$AB$或其延长线于点$M$,则有$$\lambda+\mu=\dfrac {AM}{AN}.$$当点$P$与点$B$移动到点$D$时,$AN$从$1$(正方形边长)减少到$\dfrac 14$;同时$AM$的长从$\dfrac 12$增加到$\dfrac 54$,从而得到$\lambda +\mu\in\left[\dfrac 12,5\right ]$,动图如下:
类似这样的思路可以不考虑与$AB$的交点,考虑$BF$与$AC$及其延长线的交点,由交点的位置去得到$\lambda +\mu$的值.