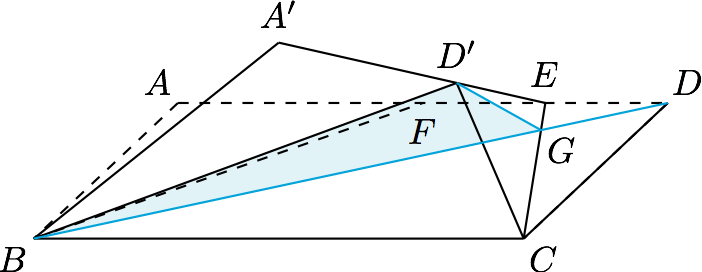
在矩形$ABCD$中，$AB=2$，$AD=4$，点$E$在线段$AD$上且$AE=3$，现分别沿$BE,CE$将$\triangle ABE,\triangle DCE$翻折，使点$D$落在线段$AE$上记为$D'$，则此时二面角$D'-EC-B$的余弦值为_______．
分析 在线段$AE$上取点$F$，使$EF=DE=1$，则折叠后$D$点与$F$点重合．接下来需要分析$D'$在平面$ECB$上投影的位置．
解 过$D$垂直于$CE$的直线为$BD$，因此折叠后的三角形$D'GB$垂直于$CE$，进而$\angle D'GB$为所求．
折叠前
由余弦定理可得$$\cos\angle D'GB=\dfrac{D'G^2+BG^2-BD'^2}{2\cdot D'G\cdot BG},$$在折叠前的图形中，即为$$\cos\angle D'GB=\dfrac{DG^2+BG^2-BF^2}{2\cdot DG\cdot BG}=\dfrac 78,$$因此所求余弦值为$\dfrac 78$．
折叠后
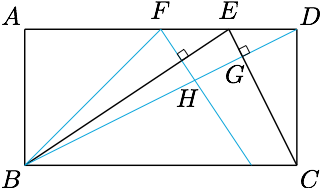
事实上，点$D'$在平面$EBC$上的投影$H$是在折叠前的矩形中$BD$与过$F$的$BE$的垂线的交点，如图．
折叠前