每日一题[63] Ptolemy定理

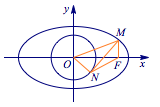
已知$F$为椭圆$\dfrac{x^2}5+y^2=1$的右焦点，第一象限内的点$M$在椭圆上，若$MF$与$x$轴垂直，直线$MN$与圆$x^2+y^2=1$相切于第四象限内的点$N$，则$NF$的长度为_______．

正确答案是$\dfrac{\sqrt{21}}{3}$．

解　如图，半通径$MF=\dfrac{b^2}{a}=\dfrac{1}{\sqrt 5}$，$OF=2$，$OM=\sqrt{\dfrac{21}5}$，$ON=1$，$MN=\dfrac{4}{\sqrt 5}$．

于是由Ptolemy定理 $$OM\cdot NF+ON\cdot MF=OF\cdot MN,$$ 代入数据计算可得 $$NF=\dfrac{\sqrt{21}}{3}.$$

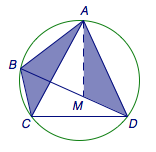
注    Ptolemy定理即圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积，可以由下图证得．作三角形$ABC$与三角形$AMD$相似，则三角形$ACD$与三角形$ABM$相似，于是有 $$BC\cdot AD=AC\cdot MD,\\AB\cdot CD=AC\cdot BM,$$ 两式相加即得．

有趣的是，当将$A,B,C,D$四点共圆的条件改为共线时，命题仍然成立（称为欧拉定理）．