这是我在QQ群高中数学试题研究中看到的题目(原题为选择题):
已知函数$f(x)$在$[0,+\infty)$上可导,其导函数记作$f'(x)$,$f(0)=-2$,且$f(x+\pi)=-\dfrac 12f(x)$.当$x\in (0,\pi)$且$x\ne\dfrac{\pi}{2}$时,$$f'(x)\cdot \cos 2x>f(x)\cdot \sin 2x-f'(x).$$若方程$f(x)+k_n\sec x=0$在$[0,+\infty)$上有$n$个解,则数列$\left\{\dfrac{n}{k_{2n}}\right\}$的前$n$项和为_______.
正确答案是$(n-1)\cdot 2^n+1$.
分析 观察题目的结构,等式$f(x+\pi)=-\dfrac 12f(x)$描述了类周期性,表明了如何通过$[0,\pi)$上的函数图象延拓出整个定义域上的图象.于是描述导函数的不等式应该是为了描述与$f(x)$有关的一个函数的单调性.根据所求问题,可以猜测关键的函数为$g(x)=\cos x\cdot f(x)$.
解 由于不等式$$f'(x)\cdot \cos 2x>f(x)\cdot \sin 2x-f'(x),$$即$$2\cos x\cdot\left(\cos x\cdot f(x)\right)'>0,$$于是令函数$g(x)=\cos x\cdot f(x)$,则$g(x)$在$\left[0,\dfrac{\pi}2\right)$上单调递增,在$\left[\dfrac{\pi}2,{\pi}\right)$上单调递减.
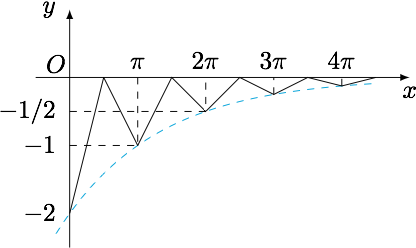
由$f(0)=-2$,且$f(x+\pi)=-\dfrac 12f(x)$可得$$g(0)=-2,g(x+\pi)=\dfrac 12g(x),$$于是函数$g(x)$的图象如图所示(为了简单起见用折线代替了曲线,虽然违反了可导,但是不影响公共点判断).
于是直线$y=-k_{2n}$与函数$g(x)$的图象有$2n$个公共点,因此$$k_{2n}=\dfrac{1}{2^{n-1}},n=1,2,\cdots ,$$从而$\dfrac{n}{k_{2n}}=n\cdot 2^{n-1}$,求和可得其前$n$项和为$(n-1)\cdot 2^n+1$.


这个题有一个问题。
易得$g’(0)>0$,由$g(x+π)=1/2g(x)$可得$g’(π)>0$。这与$g(x)$在$(π/2,π)$上单调递减且连续相矛盾。
当然$f(x)$也有对应的问题。
可以去掉不等式中$x$的取值范围中的$0$(即令$x∈(0,π/2)\cup(π/2,π)$时不等式成立),来解决这个问题。并且这样规定后,可以推得$g’(0)=0$。
谢谢!之前已经修改了此题的两个Bug,没想到还有Bug...