下面这道题目是我的好友“猴子派来的”与我讨论的题目,题目来源为2016年辽宁省实验中学,东北师大附中,哈尔滨师大附中(东北最强三校)高三第一次联合模拟考试第16题:
已知$\triangle ABC$满足$A=\dfrac{\pi}3$,$\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\cdot \overrightarrow{BC}=0$,点$M$在$\triangle ABC$外,且$MB=2MC=2$,则$MA$的取值范围是_______.
正确答案是$[1,3]$.
分析 易知$\triangle ABC$为正三角形,接下来有两条风格迥异的思路可以解决问题.
思路一 静态观察
平面上四边形的四边与对角线满足关系(托勒密定理):对角线的乘积不超过两组对边分别相乘所得乘积之和,当且仅当四边形的四个顶点共圆时两者相等.
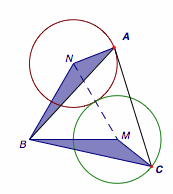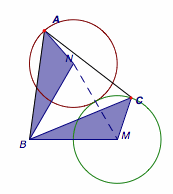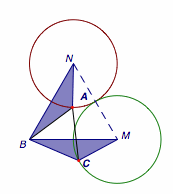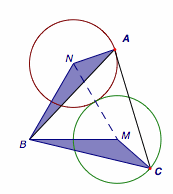
如图,设$MA=x$,$AB=BC=CA=t$,那么由左右两图分别应用托勒密定理可得$$\begin{cases} tx\leqslant 3t,\\ 2t\leqslant tx+t,\end{cases} $$于是$1\leqslant x\leqslant 3$.
由于两侧等号均能取得(如下图),又根据图形连续变化,因此$MA$的取值范围是$[1,3]$.
思路二 动态探索
如图,先固定$B,M$,使得$BM=2$,然后让$C$在半径为$1$圆$M$上运动,观察$A$点的轨迹(暂时忽略$M$在$\triangle ABC$外的条件).
由平面几何知识容易得到$A$的轨迹是圆$M$绕点$B$旋转$60^\circ$后得到的圆$N$,据此容易求得$MA$的取值范围是$[1,3]$(注意取得最值时$M$均在$\triangle ABC$外部).