有关任意量词的一个误区

已知对任意实数$x\in [0,2]$，均有$|2x-a| \geqslant x-1$成立，求$a$的取值范围．

错解

题中不等式等价于$$\begin{cases} 2x-a\geqslant 0,\\2x-a \geqslant x-1,\end{cases} \lor \begin{cases} 2x-a<0,\\ a-2x \geqslant x-1,\end{cases} $$即$$\begin{cases} a\leqslant 2x,\\a \leqslant x+1,\end{cases} \lor \begin{cases} a>2x,\\a \geqslant 3x-1 ,\end{cases} $$因此$$a \leqslant 0\lor a\geqslant 5,$$于是$a$的取值范围是$(-\infty,0]\cup [5,+\infty )$．

首先，我们用另一种方法证明上述解法得到的结果是错误的．

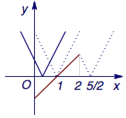
在平面直角坐标系中，画出线段$y=x-1$，$x\in [0,2]$．由于$y=|2x-a|$的图象为“V”型，最小值点为$x=\dfrac a2$，两翼的斜率分别为$\pm 2$，于是可得$a$的取值范围是$(-\infty ,2]\cup [5,+\infty )$．

接下来，我们分析错解的错误原因．不等式的同解变形应该没有问题，那么问题就出在“因此”的位置，实际上是认为命题$$t_1:\forall x\in D,\left( p(x) \lor q(x)\right) $$与命题$$t_2:\left(\forall x\in D,p(x) \right) \lor \left(\forall x\in D,q(x)\right)$$是等价的．但命题$t_2$可以推出命题$t_1$，反之则不然，也就是这样做可能会缩小参数的取值范围．

打个比方，一个班的同学，我们有

命题一：对于班上的任意同学，或者参加了长跑比赛，或者参加了跳绳比赛；

命题二：班上的任意同学都参加了长跑比赛，或者班上的任意同学都参加了跳绳比赛．

很容易得知命题二可以推出命题一，但命题一无法推出命题二．

最后，找到错误原因后该怎么改正呢？这就需要把$x$看作参数，解关于$a$的不等式了．

推理过程中的$$\begin{cases} a\leqslant 2x,\\a \leqslant x+1,\end{cases} \lor \begin{cases} a>2x,\\a \geqslant 3x-1 ,\end{cases} $$可以讨论如下：

当$0\leqslant x\leqslant 1$时，$3x-1 \leqslant 2x \leqslant x+1$，于是不等式等价于$$a \leqslant 2x\lor a>2x,$$也即$a\in\mathcal R$；

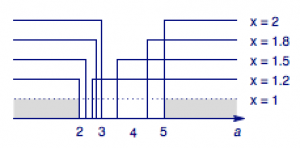
当$1<x \leqslant 2$时，$x+1<2x<3x-1$，于是不等式等价于$$a \leqslant x+1\lor a\geqslant 3x-1.$$

如图，当$x$变化时，对$a$的要求也在变化，我们需要求出可以满足所有要求的$a$的所有可能取值．

不难求得$a$的取值范围是$(-\infty ,2]\cup [5,+\infty )$．

总结   任意量词不能分配给“或”，类似的，存在量词不能分配给“且”（想一想，为什么？）．