每日一题[302] 引入参数

本题源于一道导数题，原题为求函数$f(x)=x+\sqrt{5-x^4}$的值域：

已知$a,b$均为正实数，且$a^4+b^2=5$，求$a+b$的最大值．

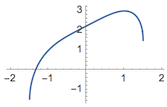
先利用导数处理函数$f(x)=x+\sqrt{5-x^4}$．

$f(x)$的定义域为$\left[-5^{\frac 14},5^{\frac 14}\right]$．

当$x<0$时，$f(x)$单调递增；

当$x\geqslant 0$时，导函数 $$\begin{split} f'(x)&=1+\dfrac 12\left(5-x^4\right)^{-\frac 12}\cdot (-4x^3)\\&=\dfrac{1}{\sqrt{5-x^4}}\cdot \left(\sqrt{5-x^4}-2x^3\right),\end{split}$$ 令 $$g(x)=\sqrt{5-x^4}-2x^3,x\geqslant 0$$ 则$g(x)$单调递减，且有唯一零点为$x=1$．

于是函数$f(x)$在$x=1$处取得极大值，亦为最大值$3$．

另一方面，函数在定义域区间端点处取得最小值，经比较可得最小值为 $$\left.y\right|_{x=-5^{\frac 14}}=-5^{\frac 14}.$$

综上，函数的值域为$\left[-5^{\frac 14},3\right]$．

接下来我们抛开导数，研究问题的核心部分，即最大值如何通过不等式知识求得．

我们知道，如果已知$a^2+b^2=5$，求$a+b$的最大值，可以通过 $$a+b=1\cdot a+1\cdot b\leqslant \sqrt{1^2+1^2}\cdot\sqrt{a^2+b^2}$$ 求得，但这里是$a^4$，就需要引入参数借助二次函数求最值了： $$\begin{split} a+b&=\dfrac{1}{\lambda}\cdot\lambda a+1\cdot b\\&\leqslant \sqrt{\left(\dfrac {1}{\lambda}\right)^2+1^2}\cdot \sqrt{(\lambda a)^2+b^2}\\&=\sqrt{\dfrac{1}{\lambda^2}+1}\cdot\sqrt{\lambda^2a^2+5-a^4}\\&=\sqrt{\dfrac{1}{\lambda^2}+1}\cdot\sqrt{-\left(a^2-\dfrac 12\lambda^2\right)^2+5+\dfrac 14\lambda^4}\\&\leqslant \sqrt{\dfrac{1}{\lambda^2}+1}\cdot\sqrt{5+\dfrac 14\lambda^4},\end{split}$$ 其中等号取得的条件为 $$\begin{cases}\dfrac{1}{\lambda}=\dfrac{\lambda a}{b},\\a^4+b^2=5,\\ a^2=\dfrac 12\lambda^2,\end{cases}$$ 解得 $$a=1,b=2,\lambda=\sqrt 2,$$ 于是所求代数式的最大值为 $$\left.\sqrt{\dfrac{1}{\lambda^2}+1}\cdot\sqrt{5+\dfrac 14\lambda^4}\right|_{\lambda =\sqrt 2}=3.$$