每日一题[305] 含参函数问题的三种处理方式

2012年高考山东卷理科数学第12题（选择压轴题）：

设函数$f(x)=\dfrac 1x$，$g(x)=ax^2+bx$（$a,b\in\mathcal R\land a\ne 0$）．若$y=f(x)$的图象与$y=g(x)$的图象有且仅有两个不同的公共点$A(x_1,y_1)$和$B(x_2,y_2)$，则下列判断正确的是（        ）

A．当$a<0$时，$x_1+x_2<0$，$y_1+y_2>0$

B．当$a<0$时，$x_1+x_2>0$，$y_1+y_2<0$

C．当$a>0$时，$x_1+x_2<0$，$y_1+y_2<0$

D．当$a>0$时，$x_1+x_2>0$，$y_1+y_2>0$

---

正确答案是 B．

我们知道，对于含参函数的零点、恒成立、存在性问题，如何处理好参数是解决问题的一大关键．一般来说，有三种不同的处理方式．

方式一    不分离，也就是将右边化为常数（往往取$0$）．注意此时可以利用$0$乘以任何数仍然为$0$对左边进行调整．

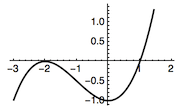
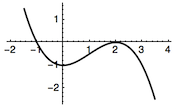
对于本题，可以将问题转化为函数

$$h(x)=ax^3+bx^2-1$$ 有两个零点，由于$h(x)$的导函数 $$h'(x)=x(3ax+2b),$$ 由$h(x)$有且仅有两个零点知$h(x)$的极值点中必有一个为零点，于是函数的两个极值点分别对应点$\left(0,-1\right)$和$\left(-\dfrac{2b}{3a},0\right)$，因此对应的函数图象如下．

当$a>0$时，如图1.

当$a<0$时，如图2.

由三次函数的切割线性质可得当$a>0$时，$x_1+x_2<0$，且

$$y_1+y_2=\dfrac 1{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1x_2}>0.$$ 当$a<0$时，$x_1+x_2>0$，且 $$y_1+y_2=\dfrac 1{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1x_2}<0,$$ 因此正确的答案是 B．

注    也可以通过三次方程的韦达定理求解．

方式二    全分离，也就是让两边分别只含参数和变量．

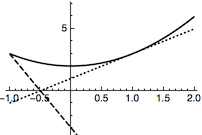
对于本题，考虑方程

$$a=\dfrac{1}{x^3}-\dfrac bx,$$ 令$t=\dfrac 1x$，并记右侧函数为 $$h(t)=t^3-bt,$$ 因此对应的函数图象如图3．

于是当$a>0$时，$y_1+y_2=t_1+t_2>0$，而

$$x_1+x_2=\dfrac 1{t_1}+\dfrac 1{t_2}=\dfrac{t_1+t_2}{t_1t_2}<0.$$ 当$a<0$时，$y_1+y_2=t_1+t_2<0$，而 $$x_1+x_2=\dfrac 1{t_1}+\dfrac 1{t_2}=\dfrac{t_1+t_2}{t_1t_2}>0,$$ 因此正确的答案是 B．

方式三    半分离，也就是将一边化为含参直线，另一边化为不含参的函数．此时问题转化为直线与曲线的位置关系问题，因此往往对曲线的凹凸性有要求．在高考范围内，只有基本初等函数和二次曲线的凹凸性可以直接使用．

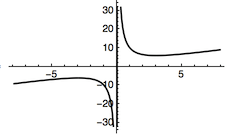
对于本题，考虑方程

$$ax+b=\dfrac{1}{x^2},$$ 于是直线$y=ax+b$与幂函数$y=x^{-2}$的图象有两个公共点．

当$a>0$时，如图4.

此时$x_1+x_2<0$，而

$$y_1+y_2=\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1x_2}>0.$$ 当$a<0$时，类似的，有$x_1+x_2>0$，而 $$y_1+y_2=\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1x_2}<0,$$ 因此正确的答案是 B．

最后给出一道练习题，请读者用三种方式处理参数．

已知不等式$x^2-2ax+2\geqslant a$对任意$x \geqslant -1$都成立，求实数$a$的取值范围．

不分离的处理方式

设函数$f(x)=x^2-2ax+2-a$，则

$$f(-1)=a+3\geqslant 0,$$ 于是 $$a\geqslant -3.$$

此时考虑对称轴$x=a$．

当$-3 \leqslant a\leqslant -1$时，函数$(x)$在$[-1,+\infty )$上单调递增，显然符合题意；

当$a>-1$时，只需要判别式

$$\Delta=4(a+2)(a-1)\leqslant 0,$$ 即 $$-2\leqslant a\leqslant 1,$$ 结合前提，有 $$-1<a\leqslant 1.$$

综上，$a$的取值范围是$[-3,1]$．

半分离的处理方式

题中不等式即

$$a(2x+1)\leqslant x^2+2,$$ 如图，斜率$a$的取值范围为$[-3,1]$．

全分离的处理方式

根据题意，有

$$\forall x\in [-1,+\infty ),x^2-2ax+2\geqslant a,$$ 即 $$\begin{cases} \forall x\in \left(-\dfrac 12,+\infty \right),a\leqslant \dfrac{x^2+2}{2x+1},\\\forall x\in\left[-1,-\dfrac 12\right),a \geqslant \dfrac{x^2+2}{2x+1},\end{cases}$$

令$t=2x+1$，则$x=\dfrac 12(t-1)$，于是

$$\dfrac{x^2+2}{2x+1}=\dfrac{t^2-2t+9}{4t}=\dfrac 14\left(t+\dfrac 9t-2\right),$$ 因此问题转化为 $$\begin{cases} \forall t\in \left(0,+\infty \right),4a+2\leqslant t+\dfrac 9t,\\\forall t\in\left[-1,0\right),4a+2\geqslant t+\dfrac 9t,\end{cases}$$

如图6，结合对勾函数$y=t+\dfrac 9t$的图象可得上式即

$$4a+2 \leqslant 6\land 4a+2\geqslant -10,$$ 即 $$-3\leqslant a\leqslant 1.$$

综上，$a$的取值范围是$[-3,1]$．