求数列通项的特征根法

递推公式描述了由数列中的已知项获得数列中新的项的方式，确定新的项所需要的已知项的数目就是递推公式的阶数．如递推公式\(a_{n}=a_{n-1}^2+a_{n-2}\)的阶数为\(2\)．要确定一个数列，通常需要给出与阶数相同的初始值，如由二阶递推公式给出的数列通常需要给定\(a_1,a_2\)的值．

如果一个数列的递推公式形如\[a_{n+2}=pa_{n+1}+qa_n,\]其中\(p,q\in\mathcal{R}\)，那么这个数列称为二阶线性递推数列．它的通项公式可以用特征根法求出．下面我们以2008年广东高考理科最后一题的数列为例看看特征根法：

例    已知\(a_1=1\)，\(a_2=\dfrac 34\)，\(a_{n+2}=a_{n+1}-\dfrac 14a_n\)，求\(a_n\)．

分析　我们希望将这个递推公式变形成可以用累加法或累乘法求通项的形式．设\[a_{n+2}-\lambda a_{n+1}=\mu(a_{n+1}-\lambda a_n),\]与递推公式对比得到\[\begin{cases} \lambda+\mu=1,\\\lambda\mu=\dfrac 14.\end{cases} \]即\(\lambda\)与\(\mu\)为一元二次方程\(x^2-x+\dfrac 14=0\)的两个根．我们将方程\(x^2=x-\dfrac 14\)称为递推公式\(a_{n+2}=a_{n+1}-\dfrac 14a_n\)的特征方程．

一般地，对于递推公式\[a_{n+2}=pa_{n+1}+qa_n\]来说，定义它的特征方程为\(x^2=px+q\)，若特征方程有两个根\(\alpha,\beta\)（可以相等，也可以为复根），则有\[\begin{cases}\alpha+\beta=p,\\\alpha \beta=-q.\end{cases}\]从而\[a_{n+2}=(\alpha+\beta)a_{n+1}-\alpha\beta a_n,\]整理得\[a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n).\]于是\[a_{n+1}-\alpha a_n=(a_2-\alpha a_1)\beta^{n-1}.\]两边同时除以\(\alpha^{n+1}\)得\[\dfrac {a_{n+1}}{\alpha ^{n+1}}-\dfrac {a_n}{\alpha^n}=\dfrac {(a_2-\alpha a_1)\beta^{n-1}}{\alpha^{n+1}}.\]再通过累加法即求得数列的通项公式．

在前面的问题中\(\alpha=\beta=\dfrac 12\)，于是得到\[a_{n+1}-\dfrac 12 a_{n}=\left(a_2-\dfrac 12 a_1\right)\left(\dfrac 12\right)^{n-1}=\left(\dfrac 12\right)^{n+1},\]从而有\[2^{n+1}a_{n+1}-2^{n}a_{n}=1，\]由累加法（或直接由\(\{2^na_n\}\)是公差为\(1\)的等差数列）得\[a_n=\dfrac {n+1}{2^n}.\]

著名的契波那契数列就是二阶线性递推数列．

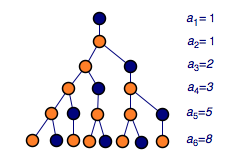
斐波那契（Fibonacci Leonardo)是意大利著名的数学家，他提出了著名的＂兔子问题＂：如果每对兔子每月繁殖一对小兔子，而这对兔子在出生后第二个月长成大兔子，并可以再繁殖一对新的小兔子，在不考虑兔子死亡的前提下，从一对小兔子开始，到第\(n\)个月共有多少对兔子．

记第\(n\)个月有\(a_n\)对兔子，那么我们就得到一个数列\(\{a_n\}\)，如图：

因为第\(n+2\)个月的兔子由两部分组成，一部分是大兔子，与第\(n+1\)个月的兔子数相同；另一部分是小兔子，是由第\(n+1\)个月的大兔子繁殖得到的，其数量正好等于第\(n\)个月的兔子数．所以有\[a_{n+2}=a_{n+1}+a_n.\]

这个数列\(\{a_n\}\)：\(1,1,2,3,5,8,13,\cdots\)就称为斐波那契数列．从第三项起，它的每一项等于前两项的和．

大家可以试试用特征根法求出它的通项公式\[a_n=\dfrac{1}{\sqrt 5}\left[\left(\dfrac {1+\sqrt 5}{2}\right)^n-\left(\dfrac {1-\sqrt 5}{2}\right)^n\right].\]虽然斐波那契数列的通项公式看上去很复杂，但别忘了它的每一项其实都是正整数．另外，波那契数列还有很多特点，比如它的前一项与后一项的比值越来越接近\(\dfrac {\sqrt 5-1}{2}\)，也就是黄金分割数，所以斐波那契数列也被称为黄金数列．