2015年高考山东卷理数解析几何大题的简解

2015年高考山东卷理科数学第20题（文科数学第21题与之基本相同）：

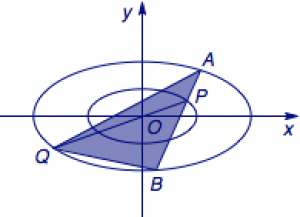
平面直角坐标系$xOy$中，已知椭圆$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）的离心率为$\dfrac{\sqrt 3}2$，左、右焦点分别是$F_1$、$F_2$．以$F_1$为圆心，以$3$为半径的圆与以$F_2$为圆心，$1$为半径的圆相交，且交点在椭圆$C$上．

（1）求椭圆$C$的方程；

（2）设椭圆$E:\dfrac{x^2}{4a^2}+\dfrac{y^2}{4b^2}=1$，$P$为椭圆$C$上任意一点，过点$P$的直线$y=kx+m$交椭圆$E$于$A$、$B$两点，射线$PO$交椭圆$E$于点$Q$．

① 求$\dfrac{|OQ|}{|OP|}$的值；

② 求$\triangle ABQ$面积的最大值．

解   （1）由椭圆的定义可得 $$2a=3+1=4,$$ 进而可以求得椭圆$C$的方程为 $$\dfrac{x^2}4+y^2=1.$$

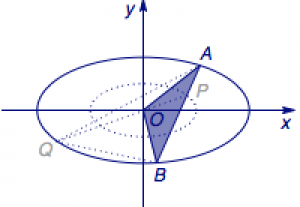
（2）① 注意到椭圆$E$与椭圆$C$的相似比是$2:1$，于是 $$\dfrac{|OQ|}{|OP|}=2,$$ 论证过程略．

② $\triangle ABQ$的三个顶点均为动点，于是直接求它的面积比较困难．注意到在运动过程中，$QO$与$OP$的比始终不变（①中的结论），于是可以得到 $$\begin{eqnarray}S_{\triangle ABQ}=3S_{\triangle ABO},\end{eqnarray}$$ 这样原来的动点$Q$就转化成了现在的定点$O$，从而简化了问题．

接下来，问题的关键是集中精力在椭圆$E$中求出$\triangle ABO$面积的最大值．需要注意的是，为了能够从这个简化的图形出发还原成原来的图形，需要直线$AB$与椭圆$C$有公共点$P$（当直线$AB$离原点$O$较远时，就无法还原了），因此在得到$\triangle ABO$的面积与$k,m$的关系之后，还需要考虑$k,m$满足的限制条件．

设$A(x_1,y_1)$，$B(x_2,y_2)$，则联立直线$AB:y=kx+m$与椭圆$E:\dfrac{x^2}{16}+\dfrac{y^2}4=1$，得 $$(4k^2+1)x^2+8kmx+4m^2-16=0,$$ 其判别式 $$\Delta_1=16(16k^2+4-m^2).$$

此时三角形$ABO$的面积为 $$\begin{eqnarray}\begin{split}S_{\triangle ABO}&=\dfrac 12\cdot |AB|\cdot d(O,AB)\\&= \dfrac 12\cdot\sqrt{1+k^2}\cdot |x_1-x_2|\cdot\dfrac{|m|}{\sqrt{1+k^2}}\\&=\dfrac 12\cdot |m|\cdot \dfrac{\sqrt{16(16k^2+4-m^2)}}{4k^2+1}\\&=2\sqrt{\dfrac{m^2}{4k^2+1}\cdot\left(4-\dfrac{m^2}{4k^2+1}\right)}.\end{split}\end{eqnarray}$$

接下来联立直线$AB$与椭圆$C$，可得 $$(4k^2+1)x^2+8kmx+4m^2-4=0,$$ 其判别式 $$\Delta_2=16(4k^2+1-m^2),$$ 由$\Delta_2\geqslant 0$可得 $$\dfrac{m^2}{4k^2+1}\in (0,1],$$ 将该范围代入(2)式中，有$S_{\triangle ABO}$的取值范围是$\left(0,2\sqrt 3\right]$，进而可得$S_{\triangle ABQ}$的最大值为$6\sqrt 3$．

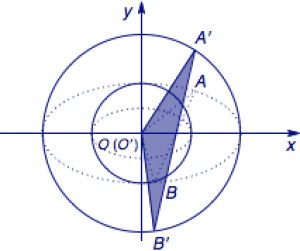
事实上，完成问题的简化后可以利用仿射变换快速确定$\triangle ABO$面积的最大值．

作保持横坐标不变，纵坐标变为原来的$2$倍的仿射变换 $$\begin{pmatrix}x'\\y'\end{pmatrix}=\begin{pmatrix}1&0\\0&2\end{pmatrix}\begin{pmatrix}{x\\y}\end{pmatrix},$$ 则椭圆$E$变为圆$E':x'^2+y'^2=16$，椭圆$C$变为圆$C':x'^2+y'^2=4$，与此同时，三角形$A'B'O'$的面积为三角形$ABO$面积的$2$倍．

设原点$O'$到弦$A'B'$的距离为$d$，则由弦$A'B'$与圆$C'$有公共点可得$d$的取值范围是$(0,2]$，于是在圆$E'$中应用垂径定理求弦长 $$|A'B'|=2\sqrt{4^2-d^2},$$ 进而 $$S_{\triangle A'B'O'}=\dfrac 12\cdot |A'B'|\cdot d=\sqrt{d^2(16-d^2)},$$ 结合$d$的取值范围可得$S_{\triangle A'B'O'}$的最大值为$4\sqrt 3$，进而可得$S_{\triangle ABO}$的最大值为$2\sqrt 3$，于是$S_{\triangle ABQ}$的最大值为$6\sqrt 3$．