双曲线有一个简单优美的结论:
双曲线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$上任意一点到两条渐近线的距离之积为定值$\dfrac{a^2b^2}{a^2+b^2}$.
直接应用点到直线的距离公式即可证明.
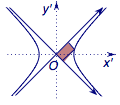
事实上,$a^2=b^2$时,双曲线为等轴双曲线,此时两条渐近线互相垂直.以两条渐近线为轴重新建立平面直角坐标系,就可以得到我们在初中经常用到的性质:过反比例函数图象上的点作坐标轴的垂线,则两条垂线与两条坐标轴所围成的矩形的面积为定值.
由于反比例函数的方程形式简单,因此很多有关等轴双曲线的问题都可以重新建立坐标系后转化为反比例函数来解决,如:
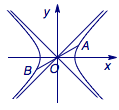
设$A$、$B$是双曲线$x^2-y^2=1$上关于原点$O$对称的两点,将坐标平面沿双曲线的一条渐近线折成直二面角,则折叠后线段\(AB\)长度的最小值为_______.
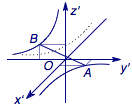
解 如图,重新建立空间直角坐标系$O-x'y'z'$.
由于双曲线的实轴长为$2$,于是在新的坐标平面$x'Oy'$上,双曲线的方程为$$x'y'=\dfrac 12,$$于是在空间坐标系中,点$A$、$B$的坐标可以分别设为$A\left(x,\dfrac 1{2x},0\right)$、$B\left(0,-\dfrac 1{2x},x\right)$.
这样,折叠后线段$AB$的长度为$$\sqrt{2x^2+\dfrac{1}{x^2}}\geqslant \sqrt{2\sqrt 2},$$等号当且仅当$x=\pm \dfrac{1}{\sqrt[4]2}$时取得,于是所求最小值为$\sqrt{2\sqrt 2}$.
下面给出一道练习题.
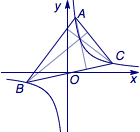
证明:等轴双曲线的内接三角形的垂心仍然在双曲线上.
注 对于一般的双曲线,也可以先通过伸缩变换转化为等轴双曲线,然后再行转化.