解析几何试题中的条件转化

这次我们来看看2010年北京高考理科数学解析几何试题中的条件转化．

在平面直角坐标系$xOy$中，点$B$与$A(-1,1)$关于原点对称，$P$是动点，且直线$AP$与$BP$的斜率之积等于$-\dfrac 13$．

（1）求动点$P$的轨迹方程；

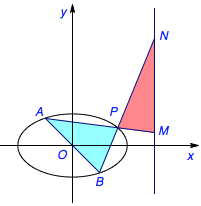
（2）设直线$AP$和$BP$分别与直线$x=3$交于点$M$，$N$，问：是否存在点$P$使得$\triangle PAB$与$\triangle PMN$的面积相等？若存在，求出点$P$的坐标；若不存在，请说明理由．

（1）动点$P$的轨迹方程为

$$\dfrac{x^2}4+\dfrac{y^2}{\dfrac 43}=1(x\neq\pm 1.$$

（2）关键条件$\triangle PAB$与$\triangle PMN$的面积相等有两种利用方式：

方式一，设点$P$ 的横坐标为$x_0$ ，则

$$\begin{split}\triangle PAB=\triangle PMN &\Leftrightarrow PA\cdot PB=PM\cdot PN\\&\Leftrightarrow \dfrac{PA}{PM}\cdot\dfrac{PB}{PN}=1\\&\Leftrightarrow \dfrac{x_0+1}{3-x_0}\cdot\dfrac{x_0-1}{3-x_0}=1\\&\Leftrightarrow x_0=\dfrac 53.\end{split}$$

方式二（由凌落蓝提供），设点$M(3,m)$，$N(3,n)$，则可以解得

$$m=4\cdot\dfrac{y_0-1}{x_0+1}+1,n=2\cdot\dfrac{y_0+1}{x_0-1}-1.$$

而根据题意

$$\begin{split}\triangle PAB=\triangle PMN &\Leftrightarrow k_{AN}=k_{BM}\\&\Leftrightarrow \dfrac{m+1}2=\dfrac{n-1}4\\&\Leftrightarrow 2\cdot\dfrac{y_0-1}{x_0+1}+1=\dfrac 12\cdot\dfrac{y_0+1}{x_0-1}-\dfrac 12\\&\Leftrightarrow y_0=-x_0\lor x_0=\dfrac 53.\end{split}$$

以下略．