如图,已知四边形$ABCD$既有外接圆又有内切圆.设四边形的四边长分别为$a,b,c,d$,内切圆圆心到四个顶点的距离分别为$a',b',c',d'$,内切圆半径为$r$.求证:$$\sin A+\sin B+\sin C+\sin D=\dfrac{8abcdr}{a'b'c'd'(a+b+c+d)}.$$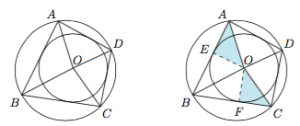
分析与解 如图,设$a=x+y,b=y+z,c=z+w,d=w+x$,则考虑到$\triangle OAE$与$\triangle COF$相似,于是有$$\tan\dfrac A2=\dfrac rx=\dfrac zr,$$类似的,有$$\tan\dfrac B2=\dfrac ry=\dfrac wr,$$这样就有\[\begin{split} \dfrac{4abcdr}{a'b'c'd'(a+b+c+d)}&=\dfrac{4r(x+y)(y+z)(z+w)(w+x)}{\sqrt{\left(x^2+r^2\right)\left(y^2+r^2\right)\left(z^2+r^2\right)\left(w^2+r^2\right)}\cdot 2\left(x+y+z+w\right)}\\
&=\dfrac{2\left(\dfrac xr+\dfrac yr\right)\left(\dfrac yr+\dfrac zr\right)\left(\dfrac zr+\dfrac wr\right)\left(\dfrac wr+\dfrac xr\right)}{\sqrt{\left(\dfrac xr\right)^2+1}\cdot \sqrt{\left(\dfrac yr\right)^2+1}\cdot \sqrt{\left(\dfrac zr\right)^2+1}\cdot \sqrt{\left(\dfrac wr\right)^2+1}\cdot \left(\dfrac xr+\dfrac yr+\dfrac zr+\dfrac wr\right)}\\
&=\dfrac{4\sin^2\dfrac{A+B}2\cdot\cos^2\dfrac{A-B}2}{2\sin\dfrac A2\cos\dfrac A2+2\sin\dfrac B2\cos\dfrac B2}\\
&=\sin A+\sin B
,\end{split} \]又$$\sin A+\sin B+\sin C+\sin D=2\left(\sin A+\sin B\right),$$因此原命题得证.
思考与总结 利用半角处理与内切圆相关的问题往往可以起到事半功倍的作用.
