2016年北京卷理科数学填空压轴题

设函数$f(x)=\begin{cases}x^3-3x,&x\leqslant a,\\-2x,&x>a.\end{cases}$

(1)若$a=0$，则$f(x)$的最大值为_______；

(2)若$f(x)$无最大值，则实数$a$的取值范围是_______．

解  $2$；$a<-1$．

此题数形结合即可．

令$g(x)=x^3-3x,\ x\in\mathcal{R}$，则 $$g'(x)=3\left(x+1\right)\left(x-1\right),$$ 故$g(x)$在$x=-1$处取得极大值$g(-1)=2$，在$x=1$处取得极小值$g(1)=-2$．

令$h(x)=-2x,\ x\in\mathcal{R}$，则$h(x)$的图象经过点$(-1,2),(1,-2)$．

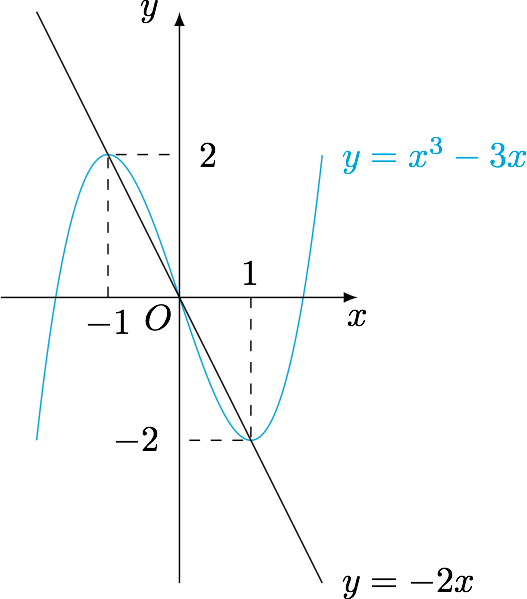
函数$g(x)$与$h(x)$的图象如下图所示，从中即可得出此题的结果．