彭赛列闭合性质

在每日一题[33]交点曲线系中，我们有：

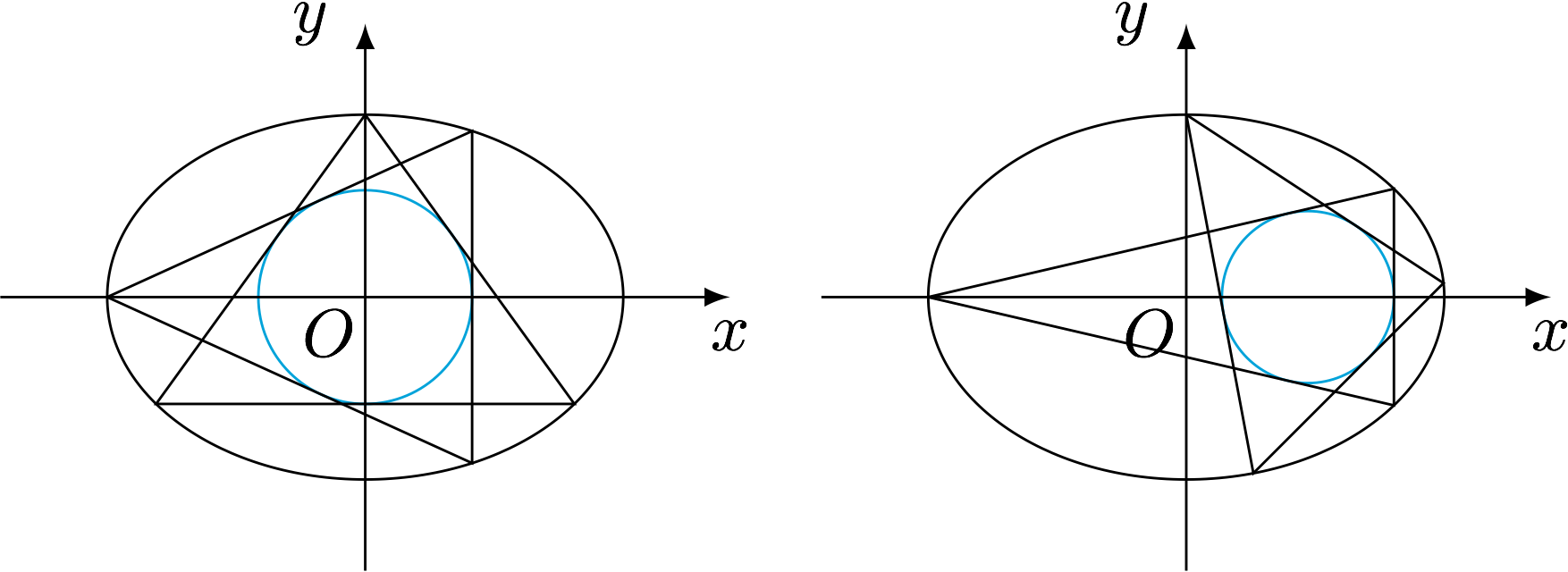
过椭圆$\dfrac{x^2}{16}+y^2=1$的左顶点作圆$(x-2)^2+y^2=\dfrac 49$的两条切线与椭圆交于另外两点，这两点的连线仍然与圆相切．事实上，这一性质对椭圆的四个顶点均成立，更进一步由彭赛列闭合性质，这一性质对椭圆上的任何一点都成立，如图．

那么对一般的椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a\neq b$)，这样的圆是否存在呢？

分析    类似于每日一题[33]的情形，利用交点曲线系处理相切关系．

解    设圆的方程为$(x-m)^2+y^2=r^2$($r>0$)，过该椭圆的左顶点与圆相切得直线为$x=t_1y-a$和$x=t_2y-a$，则由直线与圆相切的充要条件得$t_1,t_2$是关于$t$的方程$$\dfrac{|m+a|}{\sqrt{1+t^2}}=r$$的两根，方程可以化简为$$r^2t^2+r^2-(m+a)^2=$,$$于是$$t_1+t_2=0,t_1\cdot t_2=\dfrac{r^2-(m+a)^2}{r^2}.$$

将两条相交直线组成的曲线$$(x-t_1y+a)(x-t_2y+a)=0,$$即$$(x+a)^2-(t_1+t_2)(x+a)+t_1t_2y^2=0$$与椭圆$$y^2=b^2\left(1-\dfrac{x^2}{a^2}\right)$$联立可得$$r^2a^2(a+x)^2+\left[r^2-(m+a)^2\right]b^2(a^2-x^2)=0,$$将$x=m+r$带入，整理得$$(a^2-b^2)r^2+2ab^2r-b^2(m^2-a^2)=0,$$因此$$r=\dfrac{-ab^2+b\sqrt{a^4-(a^2-b^2)m^2}}{a^2-b^2}.$$特别地，将$a=4$，$b=1$，$m=2$代入可以计算得$r=\dfrac 23$，即每日一题[33]第(1)小题的计算结果．

事实上，用类似的方法可以验证，椭圆的上顶点也有上述性质．

这就意味着对一般的椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a\neq b$)，这样的圆存在，且不唯一．

注    对于椭圆$\dfrac{x^2}2+y^2=1$而言，圆$x^2+y^2=\left(2-\sqrt 2\right)^2$和圆$\left(x-\dfrac 23\right)^2=\dfrac 29$均满足要求，如图．

事实上，符合条件的圆的圆心也可以不在长轴上．采用类似的方法也可计算半径与圆心坐标的关系，但是运算量很大，不知道是否有简便算法？