函数图象作为函数的本质——数到数的映射关系的直观描述,是处理函数零点问题的最为重要和常用的手段.在各类考试中,函数的零点问题常常和函数的其他知识点综合考查,下面就常见的四种函数零点问题作一个小结.
类型一 与分段函数结合
对此类问题,一般处理方式是将函数的图象分段作出,然后分别分析函数在各个区间上的零点.
例题1 对于实数\(a\)和\(b\),定义运算“\(\ast\)”:\(a\ast b=\begin{cases}b^2-ab,a\leqslant b,\\a^2-ab,a>b,\end{cases}\)设\(f(x)=(2x-1)\ast(x-1)\),且关于\(x\)的方程\(f(x)=m(m\in\mathcal R)\)恰有三个互不相等的实数根,则\(m\)的取值范围是_______.
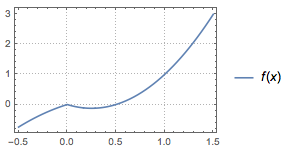
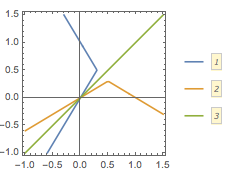
解 根据题意有\[f(x)=\begin{cases}-x^2+x,&x\leqslant 0,\\2x^2-x,&x>0,\end{cases}\]其图象如图.
容易求出\(m\)的取值范围是\(\left(-\dfrac 18,0\right)\).
类型二 与函数的周期性结合
对此类问题,一般处理方式为先集中画出函数在某个周期区间上的图象,然后再根据周期性(有时为类周期)拓展出去.
例题2 (2014年·江苏·理13)已知\(f(x)\)是定义在\(\mathcal R\)上且周期为\(3\)的函数,当\(x∈[0,3)\)时,\(f(x)=\left|x^2-2x+\dfrac 12\right|\).若函数\(y=f(x)-a\)在区间\([-3,4]\)上零点个数的所有可能取值构成的集合为________.
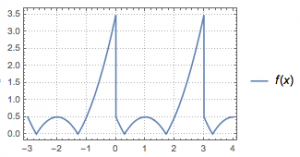
解 根据题意可以作出函数\(f(x)\)在一个完整周期区间\([0,3)\)上的图象,然后利用周期性拓展出去,如图.
于是可得函数\(y=f(x)-a\)在区间\([-3,4]\)上的零点个数为\[\begin{cases}0,&a<0,\\5,&a=0,\\10,&0<a<\dfrac 12,\\8,&a=\dfrac 12,\\4,&\dfrac 12<a<\dfrac 72,\\2,&a=\dfrac 72,\\0,&a>\dfrac 72,\end{cases}\]因此所求的集合为\(\{0,2,4,5,8,10\}\).
例题3 已知函数\(f(x)=\begin{cases}2^{-x}-1,&x\leqslant 0,\\2f(x-1),&x>0,\end{cases}\)则函数\(y=f(x)-2x\)在区间\([-5,5]\)内的零点个数为_______.
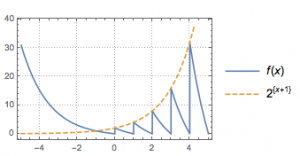
解 根据题意可以作出函数\(f(x)\)在一个完整周期区间\([-1,0)\)上的图象,然后利用类周期性拓展出去,如图.
于是所求零点个数为\(6\).
类型三 与复合函数结合
对此类问题,一般都是先求外层函数的零点,然后转化为内层函数的图象与表示外层函数零点的水平直线的交点问题.
例题4 若函数\(f(x)=x^3+ax^2+bx+c\)有极值点\(x_1,x_2\),且\(f(x_1)=x_1\),则关于\(x\)的方程\(3(f(x))^2+2af(x)+b=0\)的不同实根个数是_______.
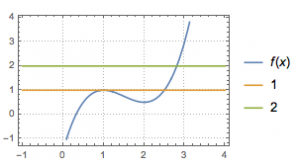
解 注意到题中方程即\[f^\prime\left(f(x)\right)=0,\]即\[f(x)=x_1\lor f(x)=x_2,\]设\(x_1<x_2\),则可以作出函数图象,如图(图中的数字表示的直线分别为\(y=x_1\)和\(y=x_2\)).
于是可得所求实根个数为\(3\).当\(x_1>x_2\)时可以类似的得到所求实根个数仍为\(3\).因此答案为\(3\).
类型四 与反函数结合
此类问题一般都以迭代函数的形式出现,解决方式有其固定思路.
例题5 已知函数\(f(x)=a\left(1-2\left|x-\dfrac 12\right|\right)\),\(a\)为常数,且\(a>0\).函数\(y=f(x)-x\)的零点称为\(f(x)\)的一阶不动点,函数\(y=f\left(f(x)\right)-x\)的零点称为\(f(x)\)的二阶不动点.若\(f(x)\)存在不为一阶不动点的二阶不动点,则\(a\)的取值范围是_______.
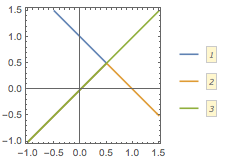
解 \(f(x)\)的一阶不动点可以看作是\(y=f(x)\)的图象与直线\(y=x\)交点的横坐标.\(f(x)\)的二阶不动点可以看作是\[\begin{cases}y=f(x),\\x=f(y),\end{cases}\]的交点的横坐标,而这两条曲线的图象是关于直线\(y=x\)对称的.因此题意为函数\(f(x)\)的图象与该图象关于直线\(y=x\)对称的图形存在直线\(y=x\)以外的交点.
当\(0<a<\dfrac 12\)时,如图.
当\(a=\dfrac 12\)时,如图.
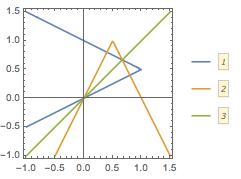
当\(a>\dfrac 12\)时,如图.
因此只有当\(a>\dfrac 12\)时符合题意,\(a\)的取值范围为\(\left(\dfrac 12,+\infty\right)\).
下面给出一组练习题.
1、已知函数\(f(x)=\begin{cases}2-|x|,x\leqslant 2,\\(x-2)^2,x>2,\end{cases}\),函数\(g(x)=3-f(2-x)\),则函数\(y=f(x)-g(x)\)的零点个数为_______.
2、已知函数\(y=f(x)\)的周期为\(2\),当\(x\in[-1,1]\)时\(f(x)=x^2\),那么函数\(y=f(x)-|\lg x|\)的零点个数为_______.
3、已知函数\(f(x)=x^2+px+q\),且函数\(y=f(f(x))\)有唯一零点,求证:\(p,q\geqslant 0\).
4、已知函数\(f(x)=\left|4-4\left|x\right|\right|-2\),求函数\(y=f(x)-x\)和函数\(y=f(f(x))-x\)的零点个数.
参考答案
1、\(2\) 提示 参考例题1.
2、\(10\) 提示 参考例题2.
3、略 提示 参考例题4.
4、\(4\),\(16\) 提示 参考例题5.