任意四面体的外接球半径公式

若四面体$ABCD$中，$\angle CAD=\alpha$，$\angle CBD=\beta$，二面角$A-CD-B$的大小为$\theta$，$CD=2m$，则其外接球半径$$R=\dfrac{m}{\sin\alpha\sin\beta\sin\theta}\cdot\sqrt{1-(\cos\alpha\cos\beta+\sin\alpha\sin\beta\cos\theta)^2}.$$

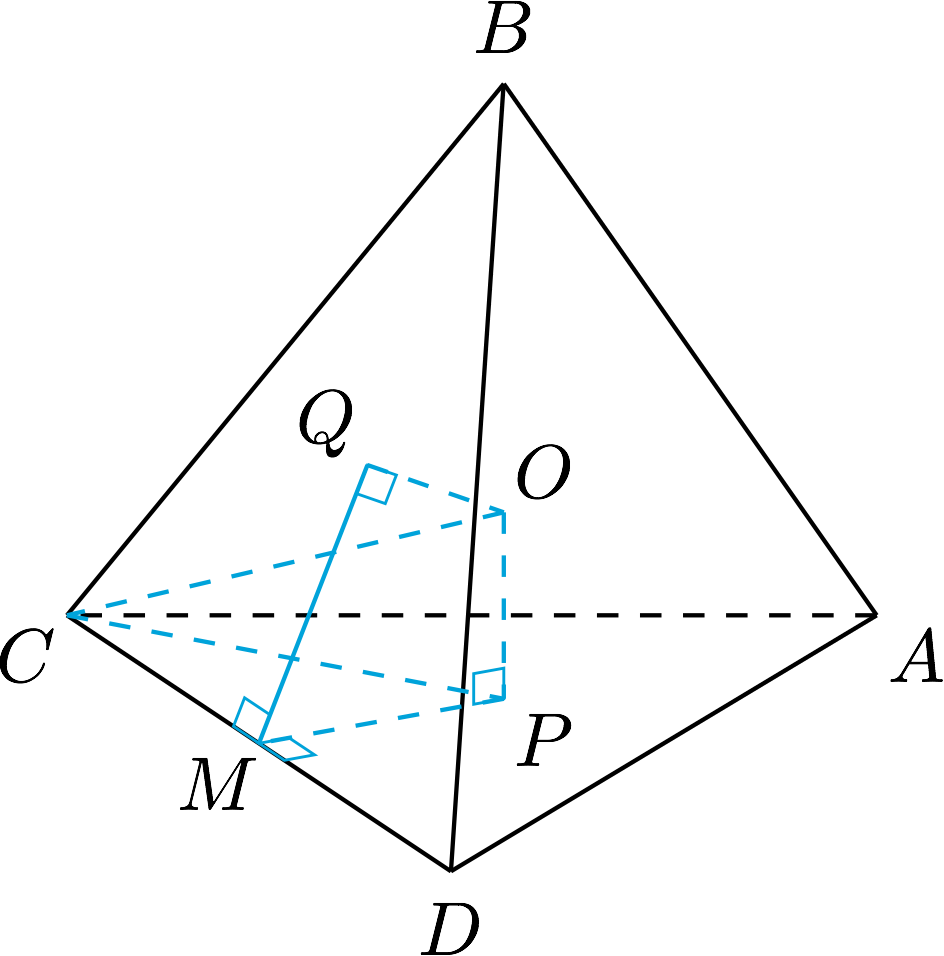
证明    如图，设$O$为四面体$ABCD$的外接球球心，$M$为$CD$的中点，$O$在平面$ACD,BCD$上的投影分别为$P,Q$，连接$OP,OQ,MP,MQ$．

显然，$P,Q$分别是$\triangle ACD$和$\triangle BCD$的外心，于是$PM\perp CD$，$QM\perp CD$，$\angle PMQ$是二面角$A-CD-B$的平面角．由于$OC=OD$，于是$OM\perp CD$，进而$O,P,M,Q$四点共面，且有$$PM=m\cot \alpha,QM=m\cot\beta,\angle PMQ=\theta.$$

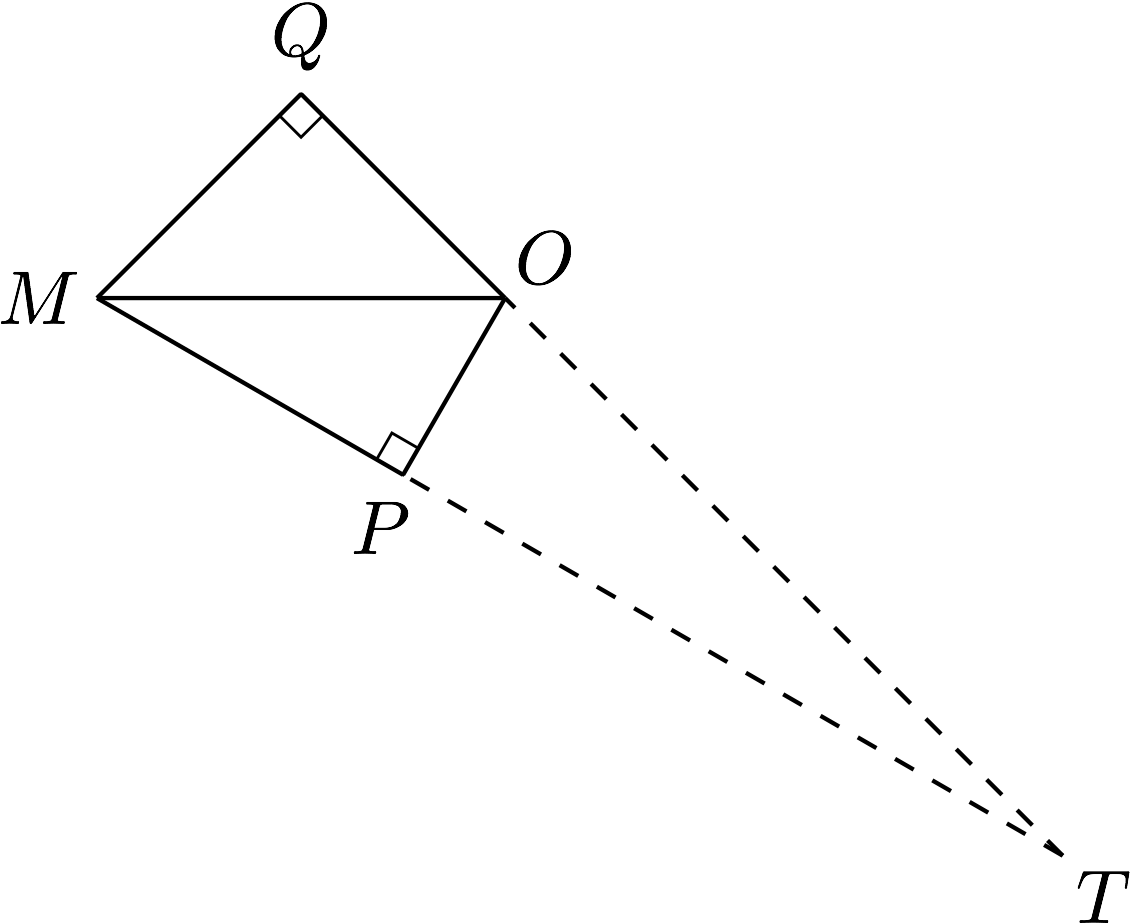
如图，延长$QO,MP$交于点$T$，则由$$\dfrac{OP}{QM}=\dfrac{TP}{TQ}$$可得$$OP=\dfrac{m}{\sin\theta}\cdot \left(\cot \alpha-\cot\beta\cdot\cos\theta\right),$$又$$PC=\dfrac{m}{\sin\alpha},$$因此由$$R^2=OC^2=OP^2+PC^2,$$代入$OP,PC$的值，整理可得$$R=\dfrac{m}{\sin\alpha\sin\beta\sin\theta}\cdot\sqrt{1-(\cos\alpha\cos\beta+\sin\alpha\sin\beta\cos\theta)^2}.$$