我们知道,平面上到两个定点的距离之比为定值$\lambda$($\lambda>0$且$\lambda\neq 1$)的点的轨迹是圆,这个圆称为阿波罗尼斯圆.当两个定点$A$和$A'$已知时,可以先在直线$AA'$上找到两点$M,N$,使得$$\dfrac{MA}{MA'}=\dfrac{NA}{NA'}=\lambda,$$然后作以$MN$为直径的圆,即得对应的阿波罗尼斯圆,如图.
反过来,如果已知其中一个定点$A$,以及动点$P$对应的阿波罗尼斯圆,也可以确定另一个定点$A'$的位置.如图,设阿波罗尼斯圆的圆心为$O$,半径为$r$,$OA=d$,$OA'=d'$,则有$$\dfrac{d-r}{r-d'}=\dfrac{d+r}{r+d'}=\lambda,$$其中$\lambda=\dfrac{PA}{PA'}$.容易解得$$\lambda=\dfrac dr=\dfrac r{d'},$$也就是说$r$是$d$和$d'$的等比中项,且公比为$\lambda$.
上述结论形式优美,容易记忆,在很多问题中可以方便的解决问题.
例一 已知$P$点在边长为$2$的正方形$ABCD$的内切圆上运动,则$AP+\sqrt 2BP$的最小值是_______.
分析与解 尝试应用阿波罗尼斯圆处理系数.连接对角线$AC$,设其中点为$O$,则可知在此问题中$r=1$,$d=\sqrt 2$,于是$d'=\dfrac{\sqrt 2}2$,且$\lambda =\sqrt 2$.
因此$$AP+\sqrt 2BP=\sqrt 2\cdot (A'P+BP)\geqslant \sqrt 2\cdot A'B,$$而在三角形$OA'B$中应用勾股定理可得$$A'B=\sqrt{OA'^2+OB^2}=\sqrt{\dfrac 52},$$因此所求的最小值为$\sqrt 5$.
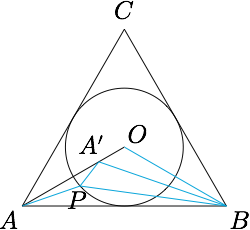
例二 已知$P$在边长为$2$的正三角形$ABC$的内切圆上运动,则$AP+2PB$的最小值是_______.
分析与解 与例一类似,$r=\dfrac{\sqrt 3}3$,$d=\dfrac{2\sqrt 3}3$,于是$d'=\dfrac {\sqrt 3}{6}$,且$\lambda =2$.
因此$$AP+2PB=2\cdot (A'P+BP)\geqslant 2\cdot A'B,$$而在三角形$OA'B$中应用余弦定理可得$$A'B=\sqrt{OA'^2+OB^2+OA'\cdot OB}=\dfrac{\sqrt {7}}{2},$$因此所求的最小值为$\sqrt 7$.
作为练习,请读者们就下面的已知条件命题:
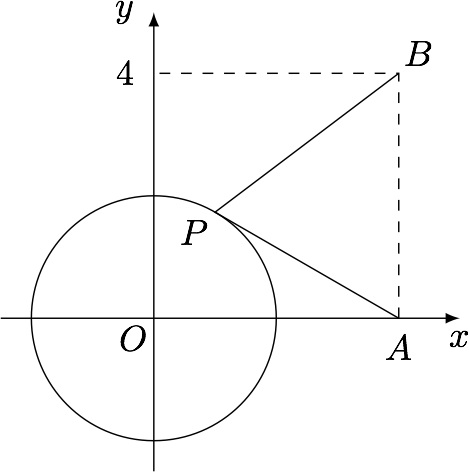
已知点$P$在圆$O:x^2+y^2=4$上运动,$A(4,0)$,$B(4,4)$,求_______的最小值.
答案是$PA+2PB$或$2\sqrt 2PA+PB$.