如图，已知等边\(\triangle ABC\)，\(\angle ABD=20^\circ\)，\(E\)是\(BD\)的中点，\(\angle CBD\)的平分线交\(CE\)于点\(F\)，连接\(DF\)．求证：\(\angle BFD=\angle ADF\)．
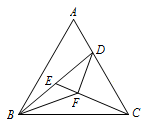
证明 如图，延长\(BF\)交\(AC\)于点\(G\)，欲证\(\angle BFD=\angle ADF\)，须证\(\angle DFG=\angle FDG\)，即求证\(DG=FG\)．
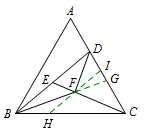过点\(F\)作\(HI\parallel BD\)，分别交\(BC,AC\)于点\(H,I\)．
由\(BF\)平分\(\angle DBC\)，可证\(BH=HF\)；
由题意可得\(\angle BDG=\angle BGD=\angle FIG\)，易证\(FI=FG=FH\)；
即\(FI=FG=FH\)．
则连接\(HG\)，可得\(HG\perp AC\)．
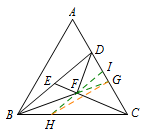所以\(HC=2GC=AD+GC\)，可得\(DG=BH=FG\)，
即可证\(\angle BFD=\angle ADF\)．