据说这是一道练习复数法的习题,但我没有用复数法解出来.
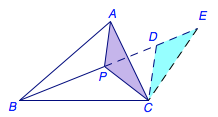
已知\(P\)为三角形\(ABC\)的费马点,记\(PA\),\(PB\),\(PC\)的长为\(x\),\(y\),\(z\),三角形的边长为\(a\),\(b\),\(c\).求证:\[(x+y+z)^2\leqslant ab+bc+ca.\]
如图,将\(\triangle APC\)旋转\(60^\circ\)到\(\triangle EDC\),则
\[\begin{split}(x+y+z)^2&=a^2+b^2-2ab\cos\left(C+\frac{\pi}3\right)\\ &=a^2+b^2-2ab\left(\frac 12\cos C-\frac{\sqrt 3}2\sin C\right)\\ &=a^2+b^2-2ab\left(\frac{a^2+b^2-c^2}{4ab}-\frac{\sqrt 3}2\cdot\frac{\sqrt{4a^2b^2-\left(a^2+b^2-c^2\right)^2}}{2ab}\right).\end{split}\]
整理,得原不等式等价于\[\left(2\sum_{cyc}ab-\sum_{cyc}a^2\right)^2\geqslant 3\left(2\sum_{cyc}a^2b^2-\sum_{cyc}a^4\right).\]
该不等式即\[\sum_{cyc}\left(a^4-ab^2c\right)\geqslant\sum_{cyc}\left(a^3b+ab^3\right).\]
此即Schur不等式当\(r=2\)时的情形.
2016年3月4日补充证法:
\[\begin{split} \sum_{cyc}{\sqrt{x^2+xy+y^2}\cdot\sqrt{x^2+xz+z^2}}&=\sum_{cyc}\sqrt{\left(\dfrac{\sqrt 3}2x\right)^2+\left(\dfrac 12x+y\right)^2}\cdot \sqrt{\left(\dfrac{\sqrt 3}2x\right)^2+\left(\dfrac 12x+z\right)^2} \\ &\geqslant \sum_{cyc}\left(\dfrac 34x^2+\dfrac 14x^2+\dfrac 12xy+\dfrac 12xz+yz\right) \\ &=(x+y+z)^2.\end{split} \]
2021年6月29日补充证法(by xixiggg):
以 $P$ 为原点,$PA$ 为实轴方向建立复平面,并记 $\omega=-\dfrac 12+\dfrac{\sqrt 3}2{\rm i}$ 为三次单位根,则 $A,B,C$ 分别对应 $x,\omega y,\omega^2z$,于是\[\begin{split} a&=|\omega y-\omega ^2z|=|y -\omega z|,\\ b&=|\omega ^2z-x|=|z-\omega x|,\\ c&=|x-\omega y|,\end{split}\]从而\[\begin{split} \sum_{\rm cyc}ab&=\sum_{\rm cyc}|y-\omega z|\cdot |z-\omega x|\\ &=\sum_{\rm cyc}|yz-\omega (z^2+xy)+\omega ^2zx|\\ &\geqslant \left|\sum_{\rm cyc}\left(yz-\omega (z^2+xy)+\omega ^2zx\right)\right|\\ &=\left|(1-\omega +\omega ^2)\sum_{\rm cyc}xy-\omega \sum_{\rm cyc}x^2\right|\\ &=\left|-2\omega \sum_{\rm cyc}xy-\omega \sum_{\rm cyc}x^2\right|\\ &=\left|-\omega (x+y+z)^2\right|\\ &=(x+y+z)^2,\end{split}\]命题得证.