平面内四点两两连线形成的六条线段的长度只有两种不同的取值$a,b$($a>b$),求$\dfrac ab$的所有可能的值.
分析与解 先不考虑$a>b$,分两种情形讨论.
第一种情形,其中存在三个点$A,B,C$构成正三角形.
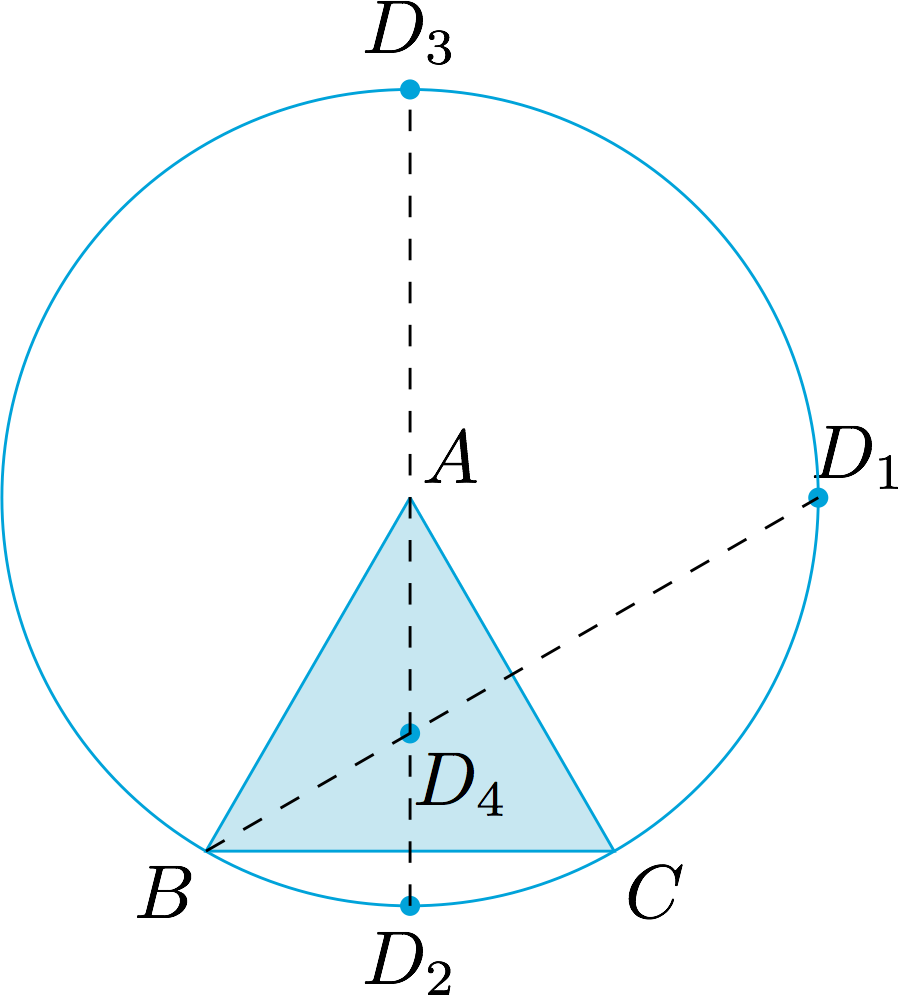
此时考虑第四个点$D$到$A,B,C$的距离,只有可能为$(a,a,b),(a,b,b),(b,b,b)$三种,对应的不同情形有四种,如图.此时所对应的比值有$\sqrt 3,\dfrac{\sqrt 6+\sqrt 2}2$.
第二种情形,其中不存在任何三点构成正三角形.
此时考虑取其中三点构成的$4$个三角形,必然存在两个三角形全等(因为只有三边长分别为$a,a,b$和$a,b,b$的两种三角形,根据抽屉原理即得).这两个全等的三角形显然均为等腰三角形,它们或者共底,或者共腰.
若全等的三角形共底$AB$,那么剩余的两个顶点必然在$AB$的垂直平分线上.显然$AC=AD=BC=BD$(否则$AC=AB$或$AD=AB$,将构成等边三角形),进而$AB=CD$(否则$\triangle ACD$为等边三角形),于是四边形$ACBD$为正方形,如图.此时对应的比值为$\sqrt 2$.
若全等的三角形共腰$AB$,此时$C,D$或者关于$AB$对称(筝形),或者关于$AB$的垂直平分线对称(等腰梯形),或者关于$AB$的中点对称(平行四边形).若$C,D$关于$AB$对称,那么$CD=AB$,则$\triangle ACD$或$\triangle BCD$为等边三角形,矛盾;若$C,D$关于$AB$的垂直平分线对称,则有两种情形;若$C,D$关于$AB$的中点对称,那么$CD=AB$,此时四边形$ACBD$为矩形,且$AC,BC,AB$两两不等,矛盾.此时对应的比值为$\dfrac{\sqrt 5+1}2$.
综上所述,所有可能的$\dfrac ab$的值为$\sqrt 3,\dfrac{\sqrt 6+\sqrt 2}2,\sqrt 2,\dfrac{\sqrt 5+1}2$.