角含半角模型之90°含45°（三）

如图，$E$是正方形$ABCD$边$CD$上一动点，$BE$的垂直平分线交对角线$AC$于点$G$，垂足为$H$，连接$BG$，并延长交$AD$于$F$，连接$EF$，若$AC=2\sqrt 2$，则$\triangle DEF$的周长为                ．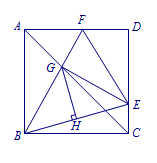

---

答案为 $4$．

法一

连接$DG$，作$GM\perp CD$，因为

$$BG=GE=GD，$$ 所以 $$\angle EGM=\angle DGM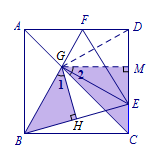，$$ 从而 $$\angle HGM=\dfrac 12\angle BGD=\angle BGC，$$ 所以 $$\angle 1=\angle 2=\angle GBE=45^\circ．$$ 故 $$EF=AF+CE．$$

法二

连接$BD$与$AC$交点为$O$，连接$OH$．则

$$OH\parallel DC．$$ 得 $$\angle 3=\angle 4=45^\circ．$$ 又 $$\angle BHG=\angle BOA=90^\circ，$$ 所以，$B、G、O、H$四点共圆，
从而 $$\angle 1=\angle 3=45^\circ．$$ 所以 $$\angle EBF=45^\circ．$$ 所以$\triangle DEF$的周长为$4$．

很多题目方法不唯一，我们要抓住图形的性质，本题中正方形的对称性就是解决这道题的关键．