已知，如图，在\(\triangle ABC\)中，\(AB=AC\)，延长\(AB\)到\(D\)，延长\(CA\)到\(E\)，连接\(DE\)，使得\(AD=BC=CE=DE\)，求\(\angle BAC\)的度数．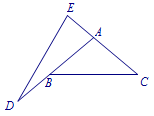
分析 此题的已知中都是线段关系，最后要求的是角的度数，很显然需要设一个角的度数为\(x\)，再根据内角和去表示其他的角度，然后再把表示的角集中在一个三角形中或特殊角中求出\(x\)，这种思路是学生们比较熟悉的，但是本题难点在于怎么去找这个三角形或特殊角．题目中给出了这么多线段相等的条件，只能是通过平移辅助，构造出三角形或特殊角．
解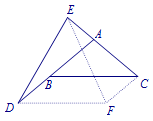
作\(DF\parallel BC\)，使得\(DF=BC\)，连接\(FC,EF\)．
设\(\angle ACB=x\)，所以\(\angle ABC=x\)，\(\angle EAD=2x\)，\(\angle E=2x\)．
由题意可得\(BCFD\)为平行四边形，
所以\(\angle BDF=\angle ABC=\angle BCF=x\)．
也可证得\(\triangle EDA\cong \triangle CEF\)，
所以\(\triangle EDF\)为等边三角形．
因为\(\angle EDF=\angle EDA+\angle ADF=180^\circ-4x+x=60^\circ\)，
所以\(x=40^\circ\)，
所以\(\angle BAC=100^\circ\)．