角含半角模型之90°含45°（一）

角含半角模型是旋转变换的一种基本模型，其中$90^\circ$含$45^\circ$是常见的一类．

模型一    如图，正方形$ABCD$中，$AD$边上一点$E$，$DC$边上一点$F$，若$\angle EBF=45^\circ$，则$AE+FC=EF$，$S_{\triangle EBF}=S_{\triangle ABE}+S_{\triangle CBF}=S_{\triangle EBF'}$．

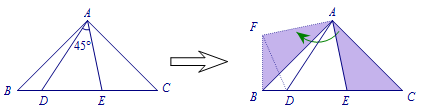
模型二    如图，等腰直角三角形$ABC$中，$\angle BAC=90^\circ$，$BC$边上两点$E、D$，若$\angle EAD=45^\circ$，则$BD^2+EC^2=DE^2$，$S_{\triangle AFD}=S_{\triangle ADE}$．

接下来，我们通过一个具体问题的解决过程介绍这一模型的应用．

例题    在正方形$ABCD$内部有两点$E、F$，$\angle EAF=\angle ECF=45^\circ$，$AB=1$，求$S_{\triangle ABE}+S_{\triangle ADF}+S_{\triangle EFC}$的值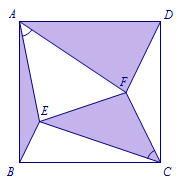． 解    可以先用找特殊位置得到答案，如下图，答案为$\dfrac 12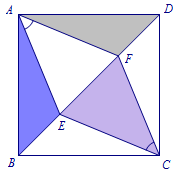$． 那么在一般位置时答案是不是不变呢？

已知条件中$\angle EAF=\angle ECF=45^\circ$，这是角含半角的模型，我们可以试着分别旋转．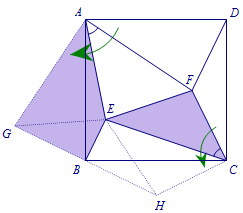

$$GB=DF=BH,\\\angle GBA+\angle ABE+\angle CBE+\angle CBH=180^\circ,\\S_{\triangle ABE}+S_{\triangle ADF}+S_{\triangle EFC}=S_{四边形AGBE}+S_{\triangle EFC}.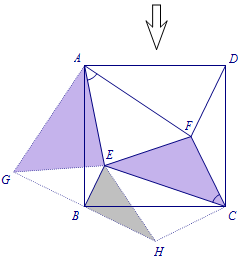$$ $$S_{四边形AGBE}+S_{\triangle EFC}=S_{\triangle AGE}+S_{\triangle EBH}+S_{\triangle EFC}.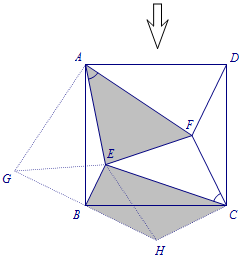$$ $$S_{\triangle AGE}+S_{\triangle EBH}+S_{\triangle EFC}=S_{\triangle AEF}+S_{\triangle EBH}+S_{\triangle EFC}.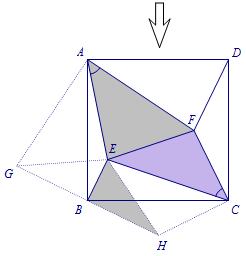$$ $$S_{\triangle AEF}+S_{\triangle EBH}+S_{\triangle EFC}=S_{四边形BECH}+S_{\triangle AEF}.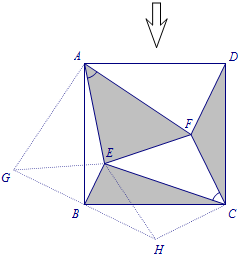$$ $$S_{四边形BECH}+S_{\triangle AEF}=S_{\triangle AEF}+S_{\triangle DFC}+S_{\triangle BEC}=\dfrac 12.$$