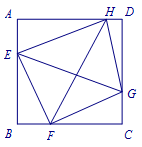
如图，\(EFGH\)是正方形\(ABCD\)的内接四边形，\(\angle BEG\)与\(\angle CFH\)都是锐角，已知\(EG=3\)，\(FH=4\)，四边形\(EFGH\)的面积为\(5\)，求正方形\(ABCD\)的面积．
分析
由已知可得\[S_{正方形ABCD}=S_{\triangle AEH}+S_{\triangle EBF}+S_{\triangle FGC}+S_{\triangle GHD}+S_{四边形EFGH}.\]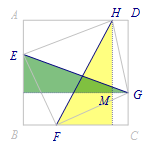
再将已知中的\(EG\)，\(FH\)利用起来，放在直角三角形中，也可得\[S_{\triangle DGH}=S_{\triangle MHG}=\dfrac 12S_{矩形DHMG}.\]
从而\[\begin{split}S_{正方形ABCD} & =2S_{\triangle EHQ}+2S_{\triangle HPG}+2S_{\triangle GNF}+2S_{\triangle EMF}+S_{矩形MNPQ}\\ &=2S_{四边形HEFG}-S_{矩形MNPQ}.\end{split}\]
解析 设\(AD=a\)，\(MN=b\)，\(NP=c\)，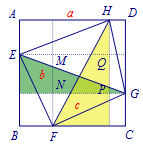 
根据题意可得\[b=\sqrt{9-a^2}，c=\sqrt{16-a^2}.\]因为\(S_{四边形MNPQ}+S_{正方形ABCD}=2S_{四边形EFGH}\)，
所以\[bc+a^2=10,\] 即\[\sqrt{9-a^2} \cdot \sqrt{16-a^2}+a^2=10,\]
解得\(a^2=\dfrac{44}{5}\)，
所以正方形\(ABCD\)的面积为\(\dfrac{44}{5}\)．